III. 2. Временные и частотные характеристики
Временные характеристики (переходная характеристика звена h (t) и весовая W (t)) систем автоматического регулировании, являющиеся, соответственно, реакциями САР на единичный скачек и единичный импульс, определяются точно так же, как и для звеньев
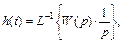
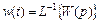 .
.
Следует отметить только, что передаточная функция W (p) САР имеют более сложный характер, чем у звеньев, и значит, нахождение оригиналов h (t) и w(t) у САР встречает большие вычислительные трудности, чем у звеньев. Поэтому для нахождения временных характеристик САР желательно воспользоваться каким-либо математическим редактором – Maple, Mathcad, Matlab и т.п.
Частотные характеристики САР находятся по той же методике, что и аналогичные характеристики звеньев. Рассмотрим более подробно построение ЛАЧХ САР с целью выработки навыков быстрого построения первой асимптоты. Отметим, что при получении ЛАЧХ САР мы будем ориентироваться, как уже говорилось ранее, не на представлении частотной передаточной функции системы в виде отношения полиномов по j 
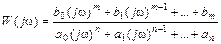 ,
,
а считать и числитель, и знаменатель этой функции произведениями комплексных функций вида 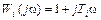 любой степени.
любой степени.
Любая частотная передаточная функция 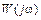 может быть отнесена к одному из трех типов. Нужно сказать, что для нахождения типа частотной передаточной функции число скобок вида
может быть отнесена к одному из трех типов. Нужно сказать, что для нахождения типа частотной передаточной функции число скобок вида 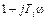 в числителе и знаменателе и их степени совсем не критичны. Тип частотной передаточной функции определяется наличием или отсутствием множителя
в числителе и знаменателе и их степени совсем не критичны. Тип частотной передаточной функции определяется наличием или отсутствием множителя 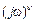 , где ν =1,2,3…, в числителе или знаменателе. Если этого множителя нет вообще, то частотная передаточная функция относится к I типу, если он находится в числителе – то ко II–му, а если в знаменателе – то к III типу. Ниже приведены примеры частотных передаточных функций, относящихся к одному из вышеуказанных типов.
, где ν =1,2,3…, в числителе или знаменателе. Если этого множителя нет вообще, то частотная передаточная функция относится к I типу, если он находится в числителе – то ко II–му, а если в знаменателе – то к III типу. Ниже приведены примеры частотных передаточных функций, относящихся к одному из вышеуказанных типов.
I. 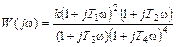 (III.2.1)
(III.2.1)
II 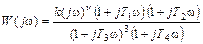 (III.2.2)
(III.2.2)
III 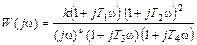 (III.2.3)
(III.2.3)
Амплитудная частотная характеристика для каждого из этих примеров различных частотных передаточных функций имеет вид
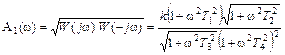 .
.
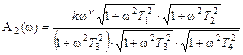 .
.
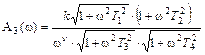 .
.
Расположим постоянные времени 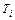 в порядке их убывания. Допустим, числовые значения параметров
в порядке их убывания. Допустим, числовые значения параметров 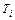 таковы, что справедливы соотношения
таковы, что справедливы соотношения 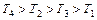 .
.
Тогда неравенства для сопрягающих частот примут вид
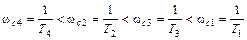 (III. 2.4)
(III. 2.4)
Для I участка частот, когда 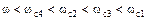 , т.е. когда
, т.е. когда  в формулах для
в формулах для  в скобках и подкоренных выражениях можно пренебречь вторыми слагаемыми по сравнению с единицей, и тогда для первой асимптоты частотной передаточной функции I, II, III типов, соответственно, получится
в скобках и подкоренных выражениях можно пренебречь вторыми слагаемыми по сравнению с единицей, и тогда для первой асимптоты частотной передаточной функции I, II, III типов, соответственно, получится
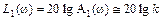 ,
,
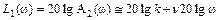 ,
,
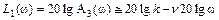 .
.
Из этих выражений следует, что для частотной передаточной функции I типа первая асимптота есть прямая линия, параллельная оси абсцисс и проходит от нее на расстоянии 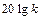 ; для частотной передаточной функции II типа первая асимптота это прямая линия с наклоном + ν 20
; для частотной передаточной функции II типа первая асимптота это прямая линия с наклоном + ν 20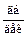 , а для частотной передаточной функции III типа – с наклоном - ν 20
, а для частотной передаточной функции III типа – с наклоном - ν 20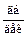 .
.
Итак, оказывается, найти первую асимптоту САР очень легко. Проведение последующих асимптот – второй, третей и т.д. – обсуждалось выше при рассмотрении упругого звена (см. III. 1.6).
Построим ЛАЧХ для частотных передаточных функций всех трех типов.
Для ЛАЧХ I типа (рис. III. 40) при, например, k = 100 первая асимптота L 1(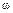 ) проходит на расстоянии
) проходит на расстоянии 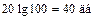 параллельно оси абсцисс. Если сопрягающие частоты подчиняются неравенствам (III. 2.4), то при частоте
параллельно оси абсцисс. Если сопрягающие частоты подчиняются неравенствам (III. 2.4), то при частоте 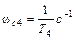 , соответствующе постоянной времени Т 4, находящейся в знаменателе (III. 2.1) в скобке со степенью ν = 2, асимптота претерпевает излом
, соответствующе постоянной времени Т 4, находящейся в знаменателе (III. 2.1) в скобке со степенью ν = 2, асимптота претерпевает излом 
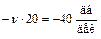 , так что наклон второй асимптоты будет
, так что наклон второй асимптоты будет 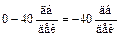 . При частоте
. При частоте 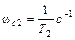 , соответствующей постоянной времени Т 2, находящейся в числителе (III. 2.1), происходит излом асимптоты на
, соответствующей постоянной времени Т 2, находящейся в числителе (III. 2.1), происходит излом асимптоты на 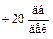 и суммарный наклон асимптоты на III участке будет
и суммарный наклон асимптоты на III участке будет 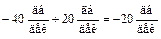 . Рассуждая аналогично предыдущему, найдем что при частоте
. Рассуждая аналогично предыдущему, найдем что при частоте 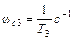 происходит дополнительный излом асимптоты на
происходит дополнительный излом асимптоты на 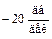 , а при частоте
, а при частоте 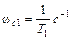 – на
– на 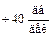 .
.
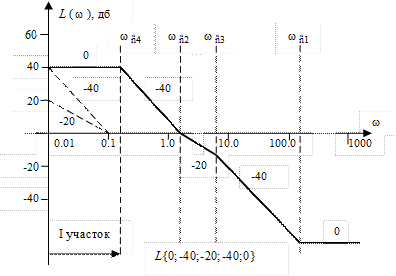
Рис. III. 40 ЛАЧХ для частотной передаточной функции САР I типа.
Для ЛАЧХ II типа при k = 0.1 и ν = 2 первая асимптота, как уже говорилось, может быть представлена в виде
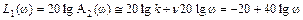 .
.
Это прямая лини с наклоном 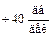 ; проходящая для любой конкретной частоты w* через точку, значение ординаты которой равно
; проходящая для любой конкретной частоты w* через точку, значение ординаты которой равно 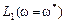 . Рекомендуется для простоты расчетов брать
. Рекомендуется для простоты расчетов брать 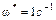 , независимо от того, принадлежит ли частота
, независимо от того, принадлежит ли частота 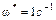 I участку или нет. Для нашего случая (рис. III.41)
I участку или нет. Для нашего случая (рис. III.41)
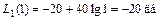 .
.
Асимптота I участка с наклоном 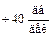 проходит через точку
проходит через точку 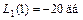 , расположенную на II участке. До сопрягающей частоты
, расположенную на II участке. До сопрягающей частоты  асимптота изображена сплошной линией, а после нее до точки
асимптота изображена сплошной линией, а после нее до точки 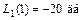 - пунктиром. На сопрягающей частоте
- пунктиром. На сопрягающей частоте  ЛАЧХ претерпевает излом на
ЛАЧХ претерпевает излом на 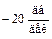 (см. III. 2.2) и суммарный наклон второй асимптоты будет
(см. III. 2.2) и суммарный наклон второй асимптоты будет 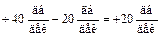 . Построение дальнейших асимптот аналогично вышерассмотренному и приведено на рис. III. 41.
. Построение дальнейших асимптот аналогично вышерассмотренному и приведено на рис. III. 41.
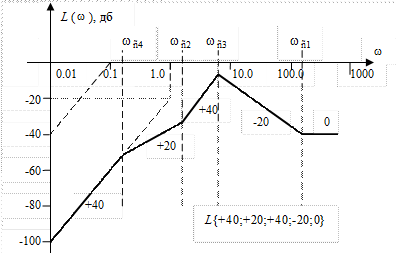
Рис. III. 41. ЛАЧХ для частотной передаточной функции САР II типа.
И, наконец, в случае частотной передаточной функции III типа при k = 0.1 и ν = 1 первая асимптота ЛАЧХ будет иметь вид
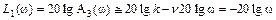 .
.
Итак, первая асимптота здесь – прямая линия с наклоном 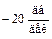 , проходящая через точку
, проходящая через точку 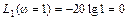 (рис. III. 42). Далее на сопрягающей частоте
(рис. III. 42). Далее на сопрягающей частоте  (см. III. 2.3) ЛАЧХ ломается на
(см. III. 2.3) ЛАЧХ ломается на 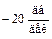 , так что наклон второй асимптоты будет
, так что наклон второй асимптоты будет 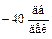 . Построение дальнейших асимптот легко уяснить из рис. III. 42 и (III.2.3).
. Построение дальнейших асимптот легко уяснить из рис. III. 42 и (III.2.3).
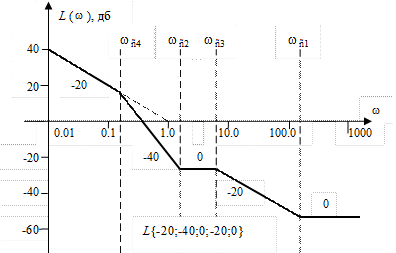
Рис. III. 42. ЛАЧХ для частотной передаточной функции САР III типа.
Итак, на этих примерах мы убедились, что построение асимптотической ЛАЧХ обходится практически без вычислений.
Не менее интересной представляется и обратная задача, часто встречающаяся при синтезе САР, - нахождение передаточной функции системы по ее заданной ЛАЧХ. Допустим, на рис. III. 43 представлена ЛАЧХ системы, передаточную функцию которой необходимо определить.
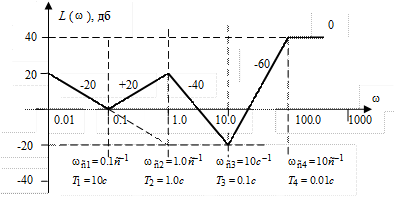
Рис. III. 43. Пример ЛАЧХ САР.
На I участке ЛАЧХ имеет наклон 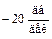 , следовательно, ее частотная передаточная функция относится к III типу и выражение для первой асимптоты имеет вид
, следовательно, ее частотная передаточная функция относится к III типу и выражение для первой асимптоты имеет вид
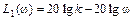 .
.
Определим неизвестный пока коэффициент усиления k. Из рис. III. 43 видно, что при 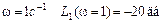 , следовательно
, следовательно
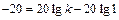 ,
,
т.е. k = 0.1, и часть передаточной функции САР, относящаяся к I участку, имеет вид
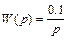 .
.
На сопрягающей частоте 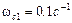 , которой соответствует постоянная времени
, которой соответствует постоянная времени 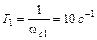 , происходит излом ЛАЧХ на
, происходит излом ЛАЧХ на 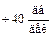 (было у первой асимптоты
(было у первой асимптоты 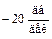 , стало у второй
, стало у второй 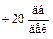 ). Отсюда следует, что часть передаточной функции САР, относящейся к первым двум участкам, будет такова
). Отсюда следует, что часть передаточной функции САР, относящейся к первым двум участкам, будет такова
 .
.
На сопрягающей частоте 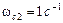 (постоянная времени
(постоянная времени 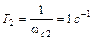 ) ЛАЧХ “ломается” на
) ЛАЧХ “ломается” на 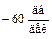 (было
(было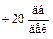 , стало
, стало 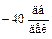 ). Это соответствует наличию в знаменателе скобки
). Это соответствует наличию в знаменателе скобки 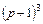 , т.е.
, т.е.
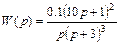 .
.
Рассуждая аналогичным образом по поводу сопрягающих частот 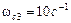 и
и 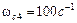 , окончательно получим для передаточной функции САР
, окончательно получим для передаточной функции САР
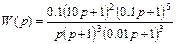 .
.
 2014-02-02
2014-02-02 1113
1113








