Замкнутые и разомкнутые САР. Одноконтурные и многоконтурные системы

Переносы сумматора и узла (разветвления сигнала).

В качестве инструмента преобразования структурных схем часто используется перенос сумматора или узла через звено (звенья) по или против хода распространения сигнала (рис. II.17 и II.18).

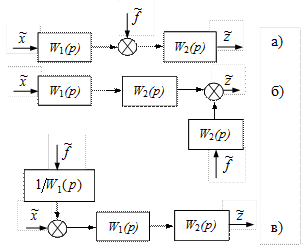
Рис. II. 17. Перенос сумматора.

На рис. II.17 а сумматор расположен между звеньями W ₁ (p) и W ₂ (p). Выходной сигнал 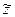состоит из двух составляющих, обусловленных сигналами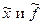

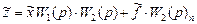(II.5.6)

Если сумматор перенести через звено W ₂ (p) по ходу распространения сигнала, то какие действия надо провести под сигналом 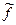, чтобы выходной сигнал 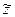не изменился? Если никаких действий не производить, то выходной сигнал 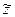в этом случае будет

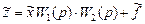
Видно, чтобы сигнал 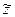совпадал с (II.5.6) надо составляющую 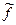пропустить через звено W ₂ (р).

Значит, при переносе сумматора через звено по ходу распространения сигнала, надо переносимый сигнал 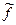умножить на передаточную функцию звена, через который переносим сумматор (рис.II.17, б).

Если перенести сумматор через звено W ₁ (p) против хода распространения сигнала, то, если никаких действий не производить над сигналом 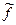, выходной сигнал 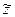будет иметь вид

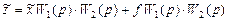
Видно, что для того, чтобы сигнал 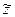не изменился по сравнению с (II.5.6) надо составляющую 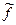пропустить через звено 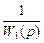(рис. II.17.6), тогда сигнал 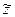будет совпадать с (II.5.6)

Проведем аналогичные рассуждения по поводу переноса узлов.

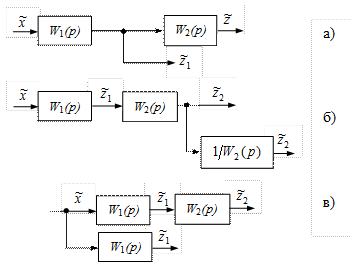
Рис. II. 18. Перенос узла.

В узле, т.е. точке ветвления сигнала, величина 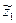(см. рис. II.18 а) будет равна

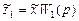(II.5.7)

Если узел перенести через звено W ₂ (р) по ходу распространения сигнала, то для того, чтобы ответвленный сигнал не изменился по сравнению с рис. II.18 а, надо его умножить на 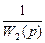. В самом деле, из рис. 18 б следует, что

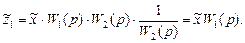
Таким образом, при переносе узла через звено W ₂ (р) по ходу распространения сигнала надо ответвляющийся сигнал умножить на .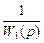

Если же узел перенести через звено W ₁ (p) против хода распространения сигнала, то, как легко понять из рис. II.18 в, надо ответвляющийся сигнал умножить на передаточную функцию W ₁ (p) звена, через которой перенесем узел.

Проведем аналогичные рассуждения по поводу переноса узлов.

Рис. II. 18. Перенос узла.

В узле, т.е. точке ветвления сигнала, величина 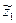(см. рис. II.18 а) будет равна

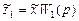(II.5.7)

Если узел перенести через звено W ₂ (р) по ходу распространения сигнала, то для того, чтобы ответвленный сигнал не изменился по сравнению с рис. II.18 а, надо его умножить на 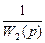. В самом деле, из рис. 18 б следует, что

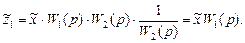
Таким образом, при переносе узла через звено W ₂ (р) по ходу распространения сигнала надо ответвляющийся сигнал умножить на .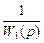

Если же узел перенести через звено W ₁ (p) против хода распространения сигнала, то, как легко понять из рис. II.18 в, надо ответвляющийся сигнал умножить на передаточную функцию W ₁ (p) звена, через которой перенесем узел.

В заключении отметим (рис.II.19), что менять местами расположенные рядом сумматоры возможно, такая же операция возможна и с узлами. Переставлять же узел и сумматор, расположенные рядом, без дополнительных манипуляций невозможно.

Рис. II. 19. Перестановка узлов и сумматоров.

Ранее замкнутая САР уже определялась как система с обратной связью. Замкнутую САР называют одноконтурной, если при ее размыкании в какой-либо точке получается разомкнутая система, состоящая из цепочки последовательно соединенных звеньев, не содержащей параллельных цепей и местных обратных связей (рис. II.20).

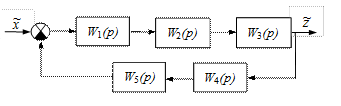
Рис. II. 20 Замкнутая одноконтурная САР.

Можно для наглядности представить замкнутую одноконтурную систему как бусы, когда на нить нанизаны бусинки – звенья САР. При размыкании САР в любом месте на этой разорванной нити будут последовательно одна к другой расположены бусинки-звенья. Передаточная функция этой последовательной цепочки звеньев, т.е. передаточная функция разомкнутой одноконтурной САР будет согласно (II.5.1) равна

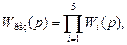
при этом передаточная функция разомкнутой системы не зависит от точки размыкания, т.к. на «нити» независимо от точки разрыва будет все то же количество «бусинок».

Для получения передаточной функции замкнутой одноконтурной САР надо по формуле (II.5.1) получить передаточную функцию прямой цепи и цепи обратной связи

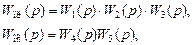
и свести дело к задаче 5.3 (рис. II.16 а).

Тогда передаточная функция замкнутой одноконтурной системы

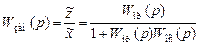
Замкнутая САР называется многоконтурной, если при ее размыкании получается цепь, содержащая параллельные или обратные связи (рис. II.21), или, иначе, замкнутая САР называется многоконтурной, если она помимо главной обратной связи содержит местные и параллельные связи.

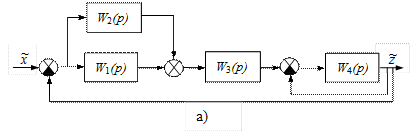
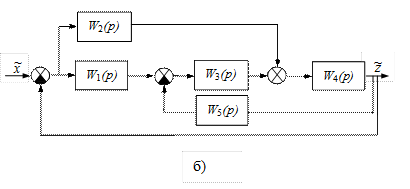
Рис. II. 21. Замкнутые многоконтурные САР.

Говорят, что многоконтурная САР имеет перекрещивающиеся связи, если контур обратной или параллельной связи. На рис. II.21.а перекрещивающихся связей нет, а на рис. II.21б звено W₃(р), принадлежащих параллельному контуру W ₁ (p), W ₂ (p), W ₃ (p), одновременно принадлежит контуру обратной связи W ₃ (p), W ₄ (p), W ₅ (p) (т.е. охватывается контуром обратной связи).

Для вычисления передаточной функции многоконтурной системы с перекрещивающимися связями необходимо прежде всего переносом узлов и сумматоров освободиться от перекрещивающихся связей. Затем, использовать эту многоконтурную систему (уже без перекрестных связей) в замкнутую одноконтурную систему, после чего определить W _раз (р) и W _зам (p) искомой системы.