Последовательное соединение звеньев

Структурных схем.

Для получения математического описания САР мы провели разбивку всей системы на отдельные элементы и записали основной закон, характеризующий протекание динамического процесса в каждом из этих элементов. Поскольку математические зависимости, описывающие процессы в элементах, носят, как правило, нелинейный характер, нам пришлось в случае несущественных нелинейностей линеаризовать эти нелинейные дифференциальные или алгебраические уравнения.

В результате этой операции мы получили столько линейных уравнений (дифференциальных или алгебраических), на сколько элементов мы разбили всю систему. Каждые из этих уравнений связывает входной и выходной сигналы элементы, а нам, поскольку мы ставим задачу получить математическое описание всей САР, необходимо уравнение, связывающее входной и выходные сигналы всей системы. Задачу можно решить, если из совокупности уравнений элементов последовательно исключать промежуточные переменные, оставив в конце концов уравнение, связывающее только входной и выходной сигналы САР. Другой, на наш взгляд, более рациональный путь заключается в таком преобразовании структурной схемы САР, чтобы из нее непосредственно можно было бы выявить связь между входным выходным сигналами системы и тем самым получить уравнение (или передаточную функцию) САР.

Для такого преобразования структурных схем необходим соответствующий набор приемов, к изучению которых мы сейчас и приступим.

Структурная схема всей исследуемой САР почти всегда содержит одну или несколько цепочек последовательно соединенных звеньев. При последовательном соединении выходная величина каждого предшествующего звена является входной величиной последующего звена (рис. II.14, а)

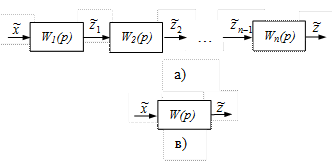
Рис. II. 14. Последовательное соединение звеньев.

Передаточные функции каждого звена цепочки 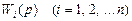известны. Требуется заменить эту цепочку одним звеном с такой передаточной функцией W(p) (рис. II.14, б), чтобы его входной 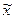и выходной 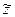сигналы остались такими же, как у рассматриваемой цепочки последовательно соединенных звеньев.

Поскольку по определению передаточной функции

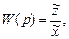
для каждого из звена цепочки получим

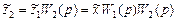
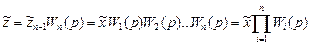
Следовательно, передаточная функция искомого заменяющего звена отсюда получится

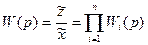(II.5.1)

Итак, передаточная функция цепочки последовательно соединенных звеньев равна произведению передаточных функций этих звеньев.

5.2. Параллельное соединение звеньев.

При параллельном соединение входная величина является общей для всех звеньев, а выходные величины звеньев алгебраически суммируются 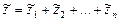(рис.II.15, а)

Требуется заменить это соединение одним звеном с такой передаточной функцией W(p) (рис. II.15 б), чтобы его входной 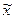и выходной 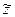сигналы остались такими же, как у данных параллельно соединенных звеньев.

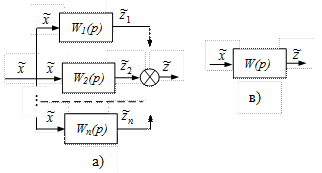
Рис. II. 15. Параллельное соединение звеньев.

Запишем согласно рис. II.15 а выходные сигналы звеньев (считая, что их передаточные функции известны) и суммируем их

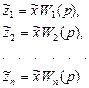
или

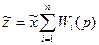
Отсюда следует, что

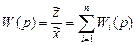(II.5.2)

Передаточная функция параллельно соединенных звеньев равна сумме передаточных функций этих звеньев.

5.3. Звенья, охваченные обратной связью.

Обозначим передаточную функцию звена или совокупности звеньев, находящихся в прямой цепи, через W ₁ (p), а в цепи обратной связи – через W ₂ (p) (рис.II.16 а).

Эти передаточные функции будем считать неизвестными. Надо найти замену этому соединению звеном с такой передаточной функцией W(p), чтобы его (звена) выходной 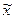и выходной 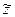сигналы совпадали с выходными соединениями

W 2 (p)

(рис. II.16г).

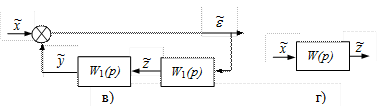
Рис. II. 16. Звенья, охваченные обратной связью.

Здесь в сумматоре сигнал может быть складываться с сигналом 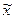(положительная обратная связь) и вычитываться из него (отрицательная обратная связь). На рис. II.16 а в цепи обратной связи расположено звено W ₂ (p), поэтому здесь имеет место неединичная обратная связь.

Нетрудно получить

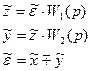
здесь верхний значок «−» относится к отрицательной обратной связи, а нижний знак «+» - к положительной.

Из этих равенств получается

или после переноса слагаемого 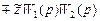в правую часть

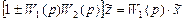
Здесь уже знак «+» относится к отрицательной, а знак «-» – к положительной обратной связи.

Отсюда

(II.5.3)

Таким образом, пе6редаточная функция звена (звеньев), охваченных обратной связью, равна дроби, в числителе которой – передаточная функция прямой цепи, в знаменателе алгебраическая сумма («+» для отрицательной, «-» для положительной обратной связи) единицы и произведения передаточной функции прямой и обратной цепей.

Рис. II.16, б переделан из рис. II.16, а с тем расчетом, чтобы получилась единичная обратная связь. При этом выходным сигналом соединения стал «у». В этом случае передаточная функция согласно вышеприведенному определению примет вид:

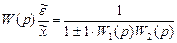(II.5.5)

где 1 во втором слагаем знаменателя – передаточная функция прямой цепи.

Из анализа соотношений (II.5.3), (II.5.4) и (II.5.5) видно, что для разных выходных сигналов системы передаточные функции различаются числителями, знаменателями же, характеризующие собственные свойства системы, везде остаются постоянными.