С. 8
С. 7
С. 6
С. 5
C. 4
.
С.2
С.1
Практикум
По заданным временным или частотным характеристикам найти передаточные функции типовых звеньев.
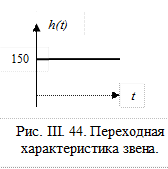 Решение.
Решение.
Нетрудно понять, что представлена переходная характеристика безынерционного звена. Из сравнения рис. III.2 и рис. III. 44 видно, что k = 150. таким образом, передаточная функция звена представленного характеристической рис. III. 44 имеет вид
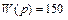 .
.
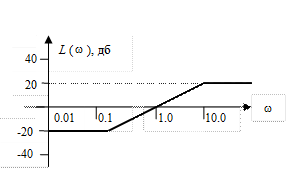
Рис. III. 45. ЛАЧХ звена.
Решение.
Представленная ЛАЧХ имеет две сопрягающие частоты 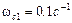 , чему соответствует постоянная времени
, чему соответствует постоянная времени 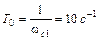 , и
, и 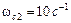 , соответствующая постоянной времени
, соответствующая постоянной времени 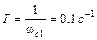 . Из рассмотренных типовых звеньев только одно (а именно упругое) имеет две постоянных времени. Из рис. III. 45 видно, что при частоте
. Из рассмотренных типовых звеньев только одно (а именно упругое) имеет две постоянных времени. Из рис. III. 45 видно, что при частоте 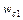 , имеет место излома ЛАЧХ на
, имеет место излома ЛАЧХ на 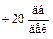 , следовательно, передаточная функция звена должна иметь в числителе сомножитель
, следовательно, передаточная функция звена должна иметь в числителе сомножитель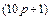 . При частоте
. При частоте 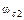 ЛАЧХ звена претерпевает излом на
ЛАЧХ звена претерпевает излом на 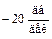 , поэтому в знаменателе передаточной функции звена должен быть сомножитель
, поэтому в знаменателе передаточной функции звена должен быть сомножитель 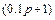 . Асимптота первого участка звена, имеющего передаточную функцию I типа, описываются зависимостью
. Асимптота первого участка звена, имеющего передаточную функцию I типа, описываются зависимостью
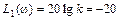 .
.
Отсюда k = 0.1. Следовательно, переходная функция рассматриваемого звена имеет вид
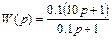 .
.
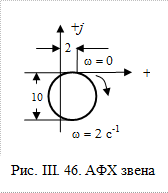 C. 3
C. 3
Решение
На рис. III. 46 представлена АФХ колебательного звена. из этого рисунки и рис. III. 31 можно получить, что k = 2; 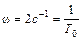 и, значит, Т0 =0.5с;
и, значит, Т0 =0.5с; 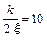 , поэтому
, поэтому 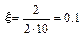 . Таким образом передаточная функция данного колебательного звена будет такова
. Таким образом передаточная функция данного колебательного звена будет такова

Решение.
Из всех типовых звеньев только одно имеет разрыв II рода АЧХ – консервативное. При сравнении рис. III. 29 и III. 47 выясняется, что 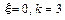 и
и 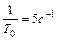 , т.е.
, т.е. 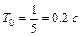 . Поэтому передаточная функция рассматриваемого консервативного звена имеет вид
. Поэтому передаточная функция рассматриваемого консервативного звена имеет вид
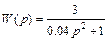 .
.
 Решение
Решение
Такую весовую функцию имеет инерционное звено. Если сравнить III. 7 и III. 48, то становится ясным, что 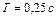 , а
, а 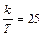 . Следовательно,
. Следовательно,
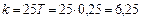
и передаточная функция звена такова
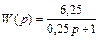 .
.
 Решение
Решение
Такую переходную характеристику имеет интегрирующее звено. Сравнивая этот рисунок с рис. III. 13, найдем, что  , т.е. k = 1. Поэтому
, т.е. k = 1. Поэтому
 .
.
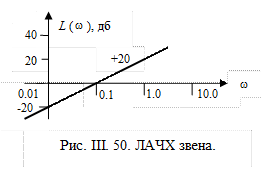
Решение.
Такая ЛАЧХ без изломов с наклоном 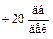 принадлежит идеальному дифференцирующему звену. Простое сопоставление этого рисунка и рис. III. 19, показывает, что
принадлежит идеальному дифференцирующему звену. Простое сопоставление этого рисунка и рис. III. 19, показывает, что 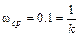 , т.е. k = 10, и передаточная функция звена
, т.е. k = 10, и передаточная функция звена
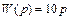 .
.
 Решение.
Решение.
Представлена характеристика реального дифференцирующего звена. Из сравнения этого рисунка с рис. III. 21 следует, что 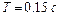 ,
, 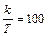 , т.е.
, т.е. 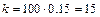 . Значит, передаточная функция реального дифференцирующего звена имеет вид
. Значит, передаточная функция реального дифференцирующего звена имеет вид
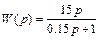 .
.
Вопросы для самопроверки.
1.Что понимают под типовым звеном?
2. Перечислите известные Вам типовые звенья и назовите их передаточные функции.
3. Какой физический смысл имеют параметра k и T инерционного звена?
4. Что такое сопрягающая частота?
5. Как определить наклон асимптоты ЛАЧХ?
6. Приведите пример реального дифференцирующего звена.
7. Какой физический смысл имеет параметр “степень затухания ξ” колебательного звена?
8. Чем отличается упругое дифференцирующее от упругого интегрирующего звена?
9. Чем отличается типы частотных передаточных функций САР?
 2014-02-02
2014-02-02 683
683








