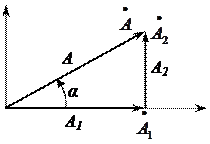2014-02-02
1446
Все графические методы расчета электрических цепей синусоидального тока не могут обеспечить высокой точности или очень сложны и трудоемки. Комплексный метод расчета, базирующийся на теории комплексных чисел, довольно прост и позволяет добиваться высокой точности. Любой вектор на плоскости изображается комплексным числом, соответствующим концу вектора.
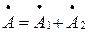, если вектор 
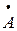разложить на составляющие А1 и А2, причем «+» означает векторное сложение. Начало вектора находится в нулевой точке числовой плоскости Гаусса, на которой, как известно, каждой точке соответствует комплексное число.
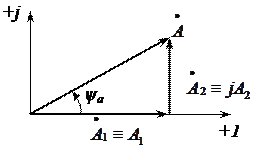
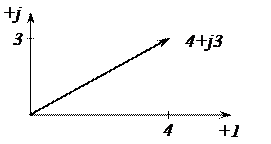
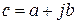
Таким образом, составляющие вектора 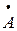могут быть представлены через его проекции А1 и А2 на действительную и мнимую оси
; 
; 
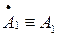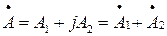
Модуль вектора 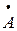, определяющий его длину, выражают равенством
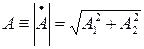
Угол, который этот вектор составляет с действительной осью, или аргумент вектора 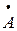определяется равенством
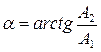
При этом составляющие мнимую и действительную нужно подставлять в равенство своими знаками.
Отсчет углов производится от действительной оси в направлении, противоположном направлении вращения часовой стрелки.
Проекции А1 и А2 можно определить при известных модуле 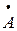и его аргументе α.
; 
.
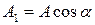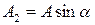Вектор 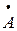в полярной форме выразится равенством
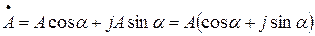
Вспомним уравнение Эйлера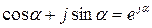 
, то получим
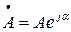
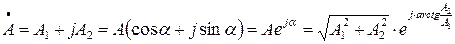
Выражение 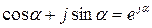называется единичным вектором, так как модуль его равен единице.
