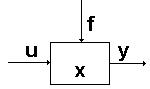
Динамический режим работы возмущающих и управляющих воздействий и является следствием инерционности элементов системы.
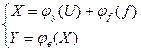
Если исключить из уравнений внутреннюю переменную Х, получим уравнение, связующее входные и выходные сигналы:
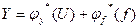
Такие математические модели называются моделями “вход-выход”. В общем случае это воздействие U и m – его производных U’, U’’, …, U(m). Управляющее воздействие f и q – его производных f’, f’’, …, f(q). Выходная величина Y и n – ее производных y’, y’’, …, y(n). Таким образом, получаем уравнение от (n+m+q+3) переменных:
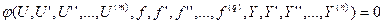
Обычно, это уравнение нелинейное, но стараются провести линеаризацию и тогда динамика линейных звеньев и систем в общем виде описывается линейным однородным дифференциальным уравнением.
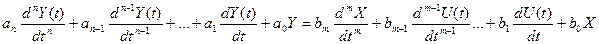 (1)
(1)
Для описания динамики звеньев существуют три основных способа:
- линейное дифференциальное уравнение;
- с помощью передаточной функции;
- с помощью частотных характеристик.
Понятие передаточной функции
Введем оператор или символ дифференцирования 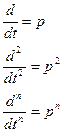
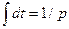
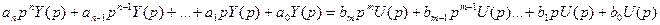
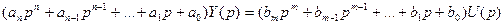 (2)
(2)
Уравнение (1) называется оригиналом, а уравнение (2) – его операторным изображением, аналогично U(t), Y(t) – оригиналы входного и выходного сигналов, а U(p), Y(p) – их операторные изображения. Была доказана связь операторной формы дифференциальных уравнений с методом интегральных преобразований Лапласса и Фурье.
Суть интегрального преобразования состоит в том, что оно преобразует некоторую функцию вещественной переменной f(t), называемую оригиналом в функцию комплексной переменной F(S). Формула интегрального преобразования Лапласса имеет вид:
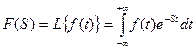 , где
, где 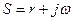 - комплексный параметр преобразований Лапласса.
- комплексный параметр преобразований Лапласса.
Если произвести преобразование Лапласса для уравнения (1), то при нулевых начальных условиях получим следующее:
 (3)
(3)
При нулевых начальных условиях операторное изображение уравнения (1) и его изображение по Лаплассу совпадает с точностью до обозначения.
Достоинство метода интегральных преобразований – преобразовываются не только функции (оригинал в изображение), но и операции над ними (дифференцирование – на умножение). В результате дифференциальное уравнение приводится к алгебраическому виду.
Из выражения (2) и (3) можно получить важную характеристику, называемую передаточной функцией:
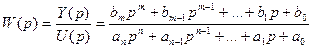
Передаточной функцией (ПФ) называется отношение операторного изображения выходной величины к входной, полученное при нулевых начальных условия:
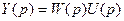
ДОМАШНЕЕ ЗАДАНИЕ: Особенности и свойства преобразований Лапласса.
 2014-02-02
2014-02-02 3107
3107








