Следящие системы

Программное управление

Стабилизация

Основные виды автоматического управления

1. Стабилизация. Системы, поддерживающие управляемую величину на заданном уровне, называется системами автоматической стабилизации. (САС). Желаемый закон управления в них имеет вид Пример САС – предыдущий пример САР генератора. Если изьять цепочку 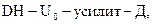то получим САС, действующую по разомкнутому принципу. Такая схема применяется, когда не требуется высокая точность стабилизации. Для более точной стабилизации регулируемой величины X применяются системы регулирования по отклонению. Известна важная особенность САР по отклонению.

Если в САР использовать регуляторы, состоящие только из элементов, обладающих аналитическими статическими характеристиками, то регулирование по отклонению может уменьшить, но не устранить ошибку.

Рассмотрим схему.

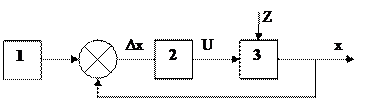Уравнения статики для такой схемы будут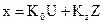

,

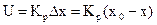где K₀, K_p, K_z – коэффициенты передачи обьекта (3), регулятора (2),

и нагрузки (Z).

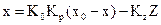
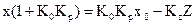
т.е. значение регулируемой величины X уменьшается с увеличением нагрузки Z. Регулирование, в котором установившаяся ошибка при постоянном значении X₀ зависит от нагрузки, называется статическим. Установившаяся статическая ошибка

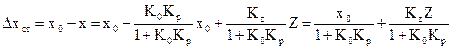
Для оценки статизма используют безразмерные отклонения 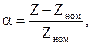где Z_ном – номинальное значение нагрузки, x_min – мин. значение

Вообще статизм δ равен относительной крутизне регулировочной характеристики

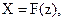
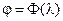, т.е.

Если характеристика F(z) прямолинейна, то

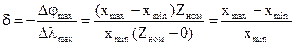
Статический регулятор поддерживает постоянное значение регулируемой величины с ошибкой.

Статизм – это величина относительно статической ошибки при изменении нагрузки от холостого хода до нормальной.

Для устранения статической ошибки используется астатическоерегулирование.

Регулировочная характеристика идеального астатического регулятора – прямая линия, параллельная оси нагрузки.

Вследствие неточности регулятора регулируемая величина может принимать любое значение внутри заштрихованной зоны. Для получения астатического регулирования в регулятор вводят астатическое звено. Примером аст. звена яв-ся интегрирующее звено, описываемое уравнением:

или .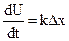

Регулятор при этом будет находиться в равновесии только тогда, когда .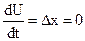

Покажем, как использование в качестве регулятора интегрирующего звена устраняет статизм САС. Рассмотрим тот же линейный объект

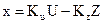(А)

Сделаем допущения

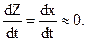(Б)

Сигнал регулятора будет равен

.

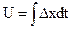Представим это выражение в уравнение (А)

.

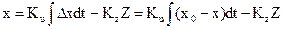Продифференцируем это уравнение по времени.

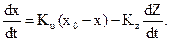
С учетом допущений (Б) это уравнение приводится к виду

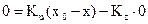
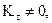
Отсюда следует, учитывая 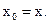А это значит погрешность стабилизации отсутствует.

2. Программное управление (ПУ). При ПУ алгоритм функционирования системы известен и можно построить задатчик программы, вырабатывающий сигнал x₀(t)= ƒ(t). ПУ можно осуществить по любому из фундаментальных принципов или с помощью их комбинаций. На практике используют два вида систем ПУ:

1) системы с временной программой;

2) системы с пространственной программой.

В системах (1) задатчик программы вырабатывает непосредственно функцию x₀(t).

Примерами могут служить устройства, в которых движение часового механизма или двигателя с равномерным ходом преобразуется с помощью функциональных преобразователей (профилированных кулачков, реостатов и т.п.) в движение x₀(t). К ним относят заводные игрушки, андроиды, магнитофоны, проигрыватели и т.д.

Системы (2) используются в программном управлении станками (ЧПУ). В них движение исполнительного органа (инструмента) осуществляется по заданной в пространстве траектории, закон движения во времени малосущественнен. При этом используются два способа пространственного ПУ:

а) движение по каждой оси осуществляется отдельным двигателем, движение по одной оси задается произвольно (обычно равномерным), а остальные движения увязываются с первым так, чтобы инструмент двигался по заданной траектории.

Пример – копировальный станок.

б) заданная траектория описывается системой параметрических уравнений, в которых параметром является время. На двигатели подаются сигналы, получаемые с помощью решающего устройства в соответствии с параметрическим уравнением.

3. Следящие системы (СС). В СС алгоритм функционирования объекта управления заранее неизвестен, т.е. x₀=? Обычно регулируемая величина в таких системах должна воспроизводить изменение некоторого фактора, следить за ним. Автоматически управляемое зенитное орудие должно поворачиваться, следя за полетом цели. СС может быть выполнена в соответствии с любым фундаментальным принципом, и будет отличаться от соответствующей системы ПУ тем, что вместо задатчика программы в СС будет помещено устройство, следящее за изменением внешнего фактора (оптический прицел).

Пример. Система отработки угла.

Регулируемой величиной является угол поворота Θ_вых управляемого объекта 2. Приводной двигатель 3 питается от электромашинного усилителя 1. Входное воздействие подается на сельсин–датчик 5 в виде угла поворота ротора Θ_вх. Соединенные по трансформаторной схеме сельсин–датчик и сельсин–приемник 4, механически связанный с нагрузкой, вырабатывают напряжение, пропорциональное рассогласованию ε=Θ_вых–Θ_вых между входным и выходным валом следящей системы. Напряжение ошибки усиливается усилителями У₁ и У₂ и ЭМУ1 и поступает на якорь исполнительного двигателя 3, вращающего одновременно объект 2 и ротор сельсин–приемника до тех пор, пока рассогласование не станет равным 0. В этом случае сельсин датчик выполняет роль задатчика, формирующего сигнал x₀.