Переходная и импульсная переходная функции
Методы анализа и синтеза линейных систем управления
Уравнения линейных систем управления
1. Анализ и синтез линейных систем управления обычно осуществляется одним из двух основных методов:
1) метод, использующий преобразованя Лапласа и Z-преобразования, передаточных функций, структурных схем и графов (частотный метод);
2) метод пространства состояний, отождествляемый с современной теорией управления. При изучении цифровых состем управления метод пространства состояний имеет следующие преимущества перед частотным методом:
- описание в пространстве состояний является естественным и удобным для решения задач на ЭВМ;
- позволяет унифицировать описание цифровых систем с различными типами квантования;
- позволяет унифицировать описание одномерных и многомерных систем;
- может применяться к некоторым типам нелинейных и нестандартных систем.
В пространстве состояний непрерывная система описывается системой дифференциальных уравнений первого порядка, называемых уравнениями состояния.
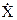 =Ax(t)+Bu(t),
=Ax(t)+Bu(t),
Y=Cx(t)+Du(t),
где A - матрица размерности nxn,
B - матрица размерности nxm,
C - матрица размерности nxq,
D - матрица размерности qxm.
Однако не должно складываться впечатления, что использование метода пространства состояния для анализа и синтеза систем управления всегда имеет очевидные преимущества. Достоинства хорошо известного частотного метода состоит в его компактности, и большое число задач проектирования реальных систем управления по-прежнему решаются с использованием методов синтеза, основанных на определении передаточной функции.
Рассмотрим в первую очередь вопросы анализа и синтеза линейных ситем управления с применением первого метода. Из теории автоматического управления известно,что совокупность технических средств(машин, орудий труда, средств механизации) выполняющих технологический процесс, является объектом управления (ОУ). Совокупность средств управления и объекта образует систему управления. Всякий ОУ характеризуется совокупностью физических величин, называемых показателями, координатами, а иногда параметрами. Необходимость в управлении значениями координат возникает в том случае, когда нормальный ход процесса нарушается из-за различного рода возмущении, т.е. колебаний нагрузки, воздействий внешней среды или внутренних помех.
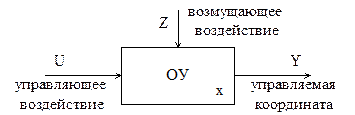
Рис. 1. Обобщенная математическая модель объекта управления x=A(Z,U).
В простейшем случае, когда А – функциональная зависимость: x=F(Z,U), и если ОУ являются безинерционным, то зависимость называют статической характеристикой ОУ.
Если ОУ обладает инерцией, то изменение координат под воздействием возмущений Z или управлений U происходят не мгновенно и в этом случае объект называют динамическим, а оператор А в этом случае является дифференциональным уравнением (или ситемой ДУ). Изменения координат в нормальном требуемом ходе технологич. процесса (ОУ) определяются совокупностью правил, предписаний или математических зависимостей, называемых алгоритмом функционирования. В ТАУ алгоритм функционирования считают заданным. Алгоритм управления будет зависеть как от алгоритма функционирования, так и от динамических свойств системы и возмущений.
Оператор А (а также структурные схемы) САУ называют её математической моделью. Такое название обусловлено тем, что при математическом описании физических процессов всегда делают какие-либо допущения и приближения.
Приведем пример академика Л.С. Понтрягина, в котором показывается, как можно математически описать движение материальной точки в трехмерном евклидовом пространстве.
Механическое состояние этой точки в каждый момент времени определяется шестью величинами: геометрическими координатамиточки x1, x2, x3, и скоростями 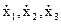 которые будут составлять векторную скорость
которые будут составлять векторную скорость 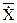 . Движение точки в пространстве определяется следующим уравнением:
. Движение точки в пространстве определяется следующим уравнением:
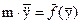 , (1)
, (1)
где m-масса точки, 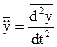 - её ускорение, а
- её ускорение, а 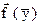 - сила, действующая на точку, которая здесь предполагается зависящей от положения
- сила, действующая на точку, которая здесь предполагается зависящей от положения 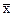 точки в пространстве. Уравнение (1) можно использовать в качестве математической модели движения летательного аппарата (ЛА). Здесь
точки в пространстве. Уравнение (1) можно использовать в качестве математической модели движения летательного аппарата (ЛА). Здесь 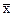 =(x1, x2, x3) – движение центра тяжести ЛА. Однако в действительности движениеЛА зависит от его ориентации в пространстве как твердого тела и тяги двигателя, которую обозначим через
=(x1, x2, x3) – движение центра тяжести ЛА. Однако в действительности движениеЛА зависит от его ориентации в пространстве как твердого тела и тяги двигателя, которую обозначим через 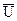 . Тогда уравнение (1) запишется в виде:
. Тогда уравнение (1) запишется в виде:
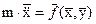 , (2)
, (2)
Величина 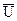 называется управлением. Выражение (2) является системой дифференциальных уравнений, которая описывает поведение объекта управления в пространстве и времени.
называется управлением. Выражение (2) является системой дифференциальных уравнений, которая описывает поведение объекта управления в пространстве и времени.
Рассмотрим далее одномерный ОУ (рис.1), поведение которого описывается дифференциальным уравнением 2-го порядка:
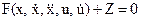 , (3)
, (3)
Это уравнение динамики системы.
Пусть при постоянных входных величинах U= U0 и Z= Z0 процесс в ОУ с течением времени установится, т.е. величина x= x0, тогда уравнение (3) примет вид:
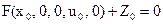 , (4)
, (4)
Это уравнение статики системы. Статическую характеристику можно построить экспериментально, подавая на вход системы постоянное воздействие и измеряя выходную величину x0 после окончания переходного процесса, или расчетным путем используя уравнение статики.
Уравнение (3) записывают в символическом виде:
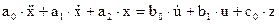 , (5)
, (5)
или в следующем виде:
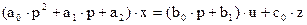 , (6)
, (6)
где 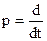 ,
,
Введем обозначения:
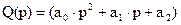 - собственный оператор,
- собственный оператор,
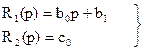 - операторы воздействия.
- операторы воздействия.
Тогда уравнение (6) можно записать в операторной форме:
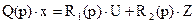 , (7).
, (7).
2. Передаточная функция.
Отношение оператора воздействия к собственному оператору называют передаточной функцией или передаточной функцией в операторной форме. ОУ (рис.1.) можно характеризовать двумя передаточными функциями:
1) по входной величине U; 2) по входной величине Z;

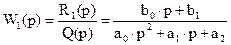 ,
, 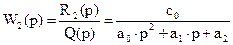 .
.
Используя передаточные функции, уравнение (5) записывают в следующем виде:
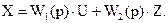
Это более компактный вид уравнения в операторной форме. Корни полиномов Q(p) и R(p) называются полюсами и нулями cоответственно. Если для некоторой передаточной функции нуль и полюс равны, то они сокращаются. В этом случае по передаточной функции нельзя восстановить дифференциальное уравнение системы и получить описание ОУ при произвольных начальных условиях.
Например. Системы описываются уравнениями:
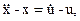
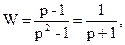
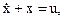
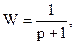
т.е. 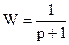 не может служить описанием системы, определяемой первым из приведенных дифференциальных уравнений.
не может служить описанием системы, определяемой первым из приведенных дифференциальных уравнений.
3. Переходная и импульсная переходная (весовая) функции.
Переходной функцией системы называют функцию, описывающую изменение выходной величины системы, когда на её вход подается единичное ступенчатое воздействие при нулевых начальных условиях. Аналитически единичное ступенчатое воздействие описывается единичной функцией:
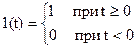
 |
Если U(t)=1(t), то x(t)=h(t). Т – время переходного процесса.
График переходной функции h(t) называется переходной или разгонной характеристикой.
Импульсной переходной или весовой функцией системы называют функцию, описывающую реакцию системы на единичное импульсное воздействие при нулевых начальных условиях. График импульсной переходной функции W(t) называют импульсной переходной характеристикой.
Переходную и импульсную переходную характеристики называют временными характеристиками.
Математически единичный импульс представляют дельта-функцией δ(t):
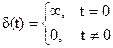
При этом должно выполнятся условие: 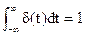 .
.
На вход подается U(t) – импульс конечной амплитуды 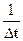 конечной длительности Δt.
конечной длительности Δt.
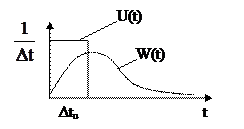
w(t) – импульсная переходная функция (весовая).
С помощью весовой функции определяется выходная координата:
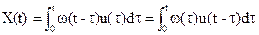
Эта формула справедлива при нулевых начальных условиях и называется сверткой функции U(t) и w(t).
Частотные характеристики системы описывают её реакцию на гармоническое воздействие.
Для линейных систем справедлив принцип суперпозиции:
Реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности, т.е. гармонический сигнал можно заменить суммой гармоник.
Это позволяет ограничиться изучением систем только с одним входом. В общем случае уравнение линейной стационарной системы с одним входом можно записать так:
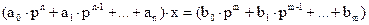 , (1)
, (1)
Передаточная функция системы:
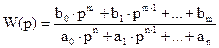 . (2)
. (2)
Функцию W(jw), которую получают из передаточной функции (2) при подстановке в неё p=jw.
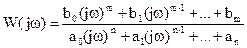 . (3)
. (3)
называют частотнойпередаточнойфункцией.
Эта функция комплексно-значная от действительной переменной w, которая называется частотой.
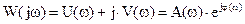 , (4),
, (4),
где 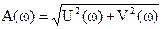 ,
, 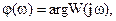 если |argW(jw)|≤
если |argW(jw)|≤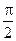 , то
, то 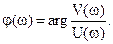
На комплексной плоскости част.перед.функц. W(jw) определяет векстор 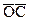 , длина которого равна A(w), а аргумент - j(w). Кривую, которую описывает конец вектора
, длина которого равна A(w), а аргумент - j(w). Кривую, которую описывает конец вектора 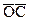 при изменении частоты w от 0 до µ (иногда -µ до µ) называют амплитудно - фазовой частотнойхарактеристикой (АФЧХ).
при изменении частоты w от 0 до µ (иногда -µ до µ) называют амплитудно - фазовой частотнойхарактеристикой (АФЧХ).
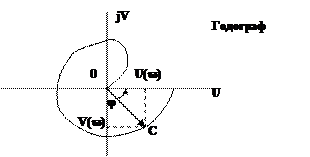 |
Частотную передаточную функцию (3) и (4) называют амплитудно - фазовойчастотной функцией. Модуль A(w) – амплитуднаячастотнаяфункция, её график – амплитуднаячастотнаяхарактеристика. Функция j(w) называется фазовой частотной функцией, а её график – фазовой частотной характеристикой (ФЧХ).
Кроме перечисленных частотных характеристик используются логарифмические частотные характеристики:
- логарифмическая амплит.част.хар-ка (ЛАЧХ);
- логарифмическая фазовая част.хар-ка (ЛФЧХ).
Назовем функцию L(w)=20lgA(w)=20lg|W(iw)| логарифмическойамплитуднойчастотнойфункцией.
График зависимости L(w) от lg(w) и есть ЛАЧХ. При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе: на отметке соответствующей значению lg(w), пишут само значение w, а не значение lg(w), а по оси ординат – значение L(w). Аналогично строится ЛФЧХ.
Единицей L(w) является децибел, а единицей логарифма частоты является декада. Декада – это интервал, на кот. частота изменяется в 10 раз. Ось ординат при построении ЛЧХ проводят через произвольную точку, а не через w=0. Частоте w=0 соответствует бесконечно удаленная точка lg(w)®-µ при w®0.
Для эксперимнтального построения частотных характеристик применяется спец. аппаратура, в состав которой входят генератор гармонических колебаний с регулируемой частотой и устройства для измерения амплитуды и фазы колебаний.
Пример. Вывести уравнение движения, опредлить передаточную функцию электродвигателя постоянного тока, управляемого изменением тока якоря. Uв и iв – напряжение и ток в обмотке возбуждения, создающие магнитный поток Фв, в котором вращается обмотка ротора (якоря) двигателя. L, R – индуктивность и омическое сопротивление обмоток якоря двигателя. Uд и iд – напряжение и ток в якорной цепи двигателя. Q - угол поворота ротора двигателя. 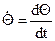 - угловая скорость.
- угловая скорость. 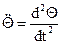 - угловое ускорение.
- угловое ускорение.
Задача решается с некоторыми допущениями: Uв=const, момент сопротивдения на валу дигателя меняется линейно от скорости.

Уравнение цепи якоря
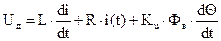 (1),
(1),
где Ku – постоянная электродвигателя по напряжению.
Уравнение вращения якоря
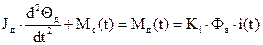 (2),
(2),
где Jд – момент инерции якоря (двигателя);
Mc – момент сопротивления (трение в подшипниках и др. потери);
Mд – движущий момент двигателя;
Ki – постоянная двигателя по току.
Поскольку мы допустили, что момент сопротивления изменяется от скорости линейно, поэтому запишем закон его изменения в виде:
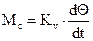 (3),
(3),
где Kv – постоянная скоростного трения двигателя.
Учитывая допущение Uв=const, положим для простоты математического выражения Фв=1.
Тогда систему уравнений (1)-(2) с учетом (3) можно записать в виде:
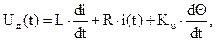
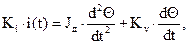
продиффиренцируем по времени второе уравнение
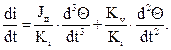
Подставим два последних уравнения в первое
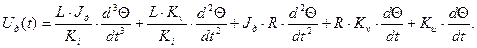
в операторной форме
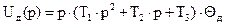 ,
,
где
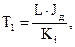
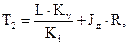
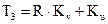 .
.
Тогда передаточная характеристика
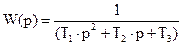
Пример 2. Найти передаточную функцию гидравлического демпфера, если пренебречь влиянием массы подвижных частей и принять за входную величину силу F, а за выходную – перемещение поршня X.
Составим уравнение равновесия сил: F=Fд, где Fд – демпфирующая сила.
|
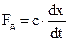
 , где с - коэффициент, зависящий от вязкости жидкости, площади поршня и др. Тогда уравнение равновесия пример вид
, где с - коэффициент, зависящий от вязкости жидкости, площади поршня и др. Тогда уравнение равновесия пример вид 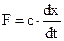 или в операторной форме
или в операторной форме 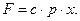
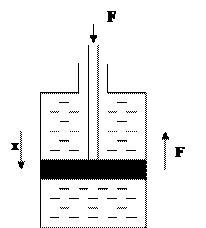 |
Если учесть массу движующихся частей, то уравнение равновесия можно записать в виде:
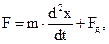 где m –масса движущихся частей
где m –масса движущихся частей
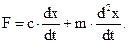 Или в операторной форме:
Или в операторной форме:
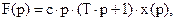
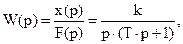 где
где 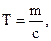
 2014-02-02
2014-02-02 1650
1650

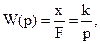 где
где