Особенности оптимальных систем программного управления и стабилизации

Оптимальное стабилизирующее управление

Пример задачи оптимального управления

Ограничения первого и второго рода

Критерий оптимальности

Постановка задачи оптимального программного управления

Понятия оптимального уравнения

1. Рассмотрим одномерный объект управления, движение которого описывается уравнением

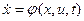(1),

где x – состояние объекта,

u – управление,

φ – заданная функция, которая предполагается непрерывной и необходимое число раз дифференцируемой по x,u, и t.

В уравнении (1) управление является неизвестной функцией времени, которая определяется исходя из следующих условий.

а) Задано начальное и конечное состояние объекта управления

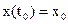, (2)

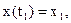(3)

где t₀ и t₁ – времена начала и конца функционирования объекта.

Часто краевые условия (2) и (3) имеют более общий вид:

- моменты времени t₀ и t₁, не заданы (либо один из них не задан), тогда говорят о задаче с нефиксированным временем;

- не задано начальное состояние x₀ (задача со свободным левым концом траектории) с фиксированным или нефиксированным временем;

- не задано конечное состояние x₁ (задача со свободным правым концом);

- не заданы x₀ и x₁, но заданы их множества возможных значений (задача с подвижными концами).

б) Эффективность управления оценивается с помощью интеграла

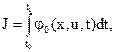(4)

где φ(x,u,t) – заданная непрерывная функция своих аргуметов.

Для определенности будем полагать, что эффективность управления тем выше, чем меньше значение этого интеграла. Тогда выражение (4) примет вид

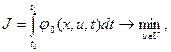(5)

где U – множество допустимых управлений.

Выражение (5) называется критерием оптимальности.

в) На управления и переменные состояния накладывается ограничения, выражающие ограниченные ресурсы управления и допустимые пределы изменения переменных состояния. Часто эти ограничения имеют вид:

где x^* и u^* - заданные предельные значения переменных x и u.

Задачу оптимального управления можно сформулировать следующим образом:

Необходимо найти оптимальное управление 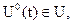при которых объект (1) переводится из состояния (2) в состояние (3), выполняются ограничения (6) и при этом функционал (4) принимает наименьшее значение. Функцию 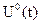называют оптимальным програмным управлением.

2. Критерии оптимальности типа (5) называется скалярными, если они представляют только один частный критерий из совокупности всех критериев, характеризующих качество систем управления. Различают три вида критериев оптимальности:

1) критерий оптимальности по – быстродействию;

2) критерий оптимальности по – точности;

3) все остальные критерии.

В качестве критерия оптимальности по – быстродействию может быть принято время переходного процесса:

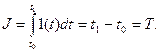(7)

Полученная при этом система является оптимальной по–быстродействию, если обеспечивается минимум интеграла (7) с учетом ограничений.

В качестве критерия оптимальности по–точности может быть интегральная оценка качества переходного процесса.

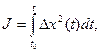(8)

где Δx – отклонение фактического состояния x от заданного .

Полученная по минимуму интеграла (8) система является оптимальной по–точности в динамических режимах при ненулевых начальных условиях или единичном задающем воздействии.

В качестве критерия оптимальности, относящегося к третьему виду, можно использовать критерий, характеризующий расход энергии на управление. Для электрического источника энергии он будет иметь вид

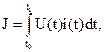(9)

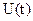где и 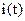- напряжение и ток нагрузки источника.

Полученная из условия минимума функционала (9) система является оптимальной по расходу энергии на управление.

3. Ограничения (6) делят на два типа:

1) ограничения 1-го рода (естественные ограничения) обусловлены принципом работы объекта. Например, частота вращения асинхронного двигателя не может быть больше синхронной; выходные сигналы усилителей ограничены из-за явления насыщения;

2) ограничения 2-го рода (условные ограничения), которые вводят сознательно. Например, величину тока якоря электродвигателя постоянного тока ограничивают условиями начальной коммутации на коллекторе, нагревом токоведущих частей, предельной температурой изоляции обмоток.

В ряде случаев ограничения задаются в виде функционалов. Так, ограничения на нагрев двигателя постоянного тока определяются интегралом

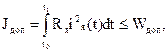
где 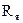- сопротивление обмотки якоря двигателя.

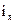- ток якоря,

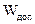- допустимая энергия, расходуемая на нагрев двигателя.

При оптимизации технологических процессов принимают определенные ограничения экономического характера, накладываемые на производительность, качество и себестоимость продукции, и т.д.

4. В качестве примера задачи оптимального программного управления рассмотрим задачу управления силовой частью электрического привода типа “двигатель–генератор”.

Здесь E₁, i₁ – напряжение в обмотке возбуждения генератора Г,

E₂, i₂ – напряжение в обмотке возбуждения двигателя Д

1) Уравнение моментов на валу двигателя

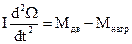(10)

I – момент инерции якоря двигателя и приводимости в движение рабочего механизма (Р.М.),

Ω – угол поворота двигателя,

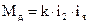- момент нагрузки

2) Уравнение якорной цепи

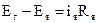(11)

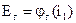- Э.Д.С. генератора,

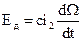- Э.Д.С. двигателя, с – коэффициент пропорциональности.

Подставим E_г и E_д в (2)

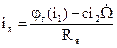(12)

3) Уравнения цепей возбуждения генератора и двигателя

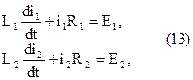
Возможны следующие режимы управления Р.М.

а) за min время разогнатся до заданной скорости,

б) совершить заданную работу за min время,

в) переместить механизм из одного положения в другое за заданное время при min потерях в цепях управления и якорной цепи.

Осуществление каждого из этих режимов управления затруднено целым рядом ограничений.

1. Перегрев якоря зависит от тока в цепи якоря.

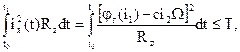(14)

где T – допустимая температура.

2. Напряжение E₁ и E₂ ограничены напряжением источников питания – E₁₀, E₂₀:

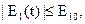
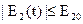(15)

3. Max значение скоростей и ускорение движения ограничены из условий прочности Р.М., либо комфорта.

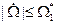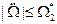, , (16)

где 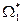и - заданные числа.

Критерий эффективности режимов “а” и “б”

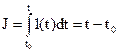(17)

Начальными и конечными состояниями системы “генератор–двигатель” является положение Ω и частота вращения 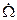вала двигателя, ток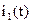и и 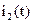в начальный 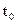и конечный 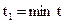моменты времени

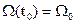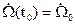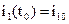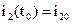, , , (18)

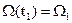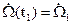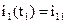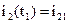, , , (19)

Оптимальным программным управлением являются законы изменения напряжений E₁(t) и E₂(t), удовлетворяющих ограничениям (15), при которых система “генератор–двигатель” переходит из состояния (18) в состояние (19) и при этом функционал (17) принимает min значение и выполняются ограничения (14) и (16). Для режима “в” минимизируемый фнкционал имеет вид:

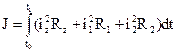
Для удобства запишем уравнение системы “генератор–двигатель” с учетом следующих обозначений

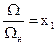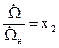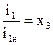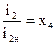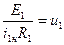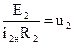, , , , , (20)

Для простоты положим, что численное значение 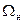и 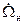равны, т.е. 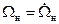, тогда .

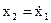Из (10)

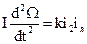с учетом (12)

, ,

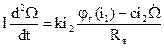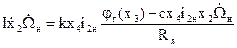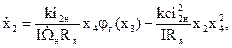Пусть , .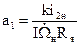

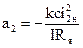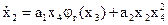
Из (13)

,

,

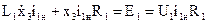
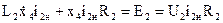
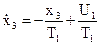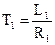
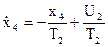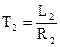
Таким образом, уравнения системы

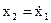
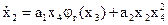
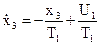
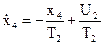
оптимальным программным управлением, например, для режима “а”, будут функци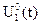и и 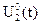, такие, что Р.М. за минимальное время переместится из состояния 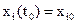, 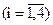в состояние ,

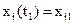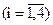
где

, , , , , .

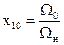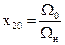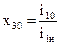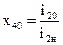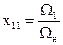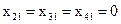5. Пусть оптимальное программное управление найдено. Это означает, что известна функция 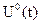. Подставляя ее в уравнение (1) и решая уравнение с начальными условиями (2) и (3), получим функцию 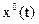, которую будем называть оптимальным программным движением или оптимальной программной траекторией. Реальное (истинное) движение системы всегда отличается от программного по следующим причинам

а) неточная реализация начальных условий (2) и (3);

б) неполная информация о внешних возмущениях, действующих на систему;

в) неточная реализация программного управления и т.д.

Поэтому реальное движение описывается функциями:

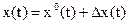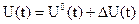, , (21)

где Δx(t) – отклонение (возмущение) фактического движения от программного,

ΔU(t) – отклонение реального управления от программного.

О погрешности Δx(t) известно лишь, что она удовлетворяет неравенству

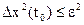, (22)

где ε – известное число.

Подставим выражение (21) в уравнение (1):

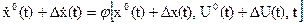(23)

Вычтем из уравнения (23) тождество

.

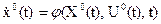В результате получили уравнение возмущенного движения

.

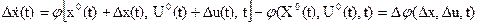Если функцию 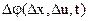разложить в ряд Тейлора в окрестности точки 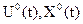, то уравнение примет вид:

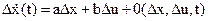, (24)

где 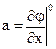, 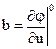(знак означает, что частные производные вычисляются в т. )

Отбрасывая в (24) нелинейные члены, получим уравнение первого приближения

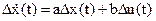(25).

Решение уравнения (25) при начальных условиях (2) и (3) описывает отклонение реального движения от программного в каждый момент времени. Для количественной оценки этих отклонений используют значение интеграла

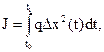(26)

где q – положительное число.

Интеграл (26) характеризует “расстояние” реального движения от программного и является мерой близости этих движений.

Используем ΔU(t) для сближения этих движений, тогда ΔU(t) называется стабилизирующим управлением. Таким образом, результирующее управление 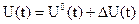состоит из программного и стабилизирующего управлений. Подставляя это выражение в (6), получим ограничение на стабилизирующее уравнение

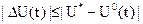. (27)

Обычно 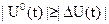. Это объясняется тем, что программное управление обеспечивает основное (программное) движение системы, а стабилизирующее управление лишь компенсирует малые отклонения от программного движения, обеспечивая требуемую точность осуществления программного движения. В связи с этим часто вместо ограничений (27), определяющих допустимый “расход” стабилизирующего управления в каждый момент времени, накладывают на стабилизирующие управления интегральные ограничения (ограничения на “энергию” управлений).

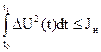. (28)

С учетом ограничений (28) будем вместо (26) рассматривать критерий качества стабилизации

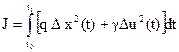(29)

где γ – определяется значеним J_u.

Стабилизирующее управление предназначено для минимизации интеграла (29) и определяется как функция переменной состояния и времени

ΔU(t)=ƒ[Δx(t),t]. (30).

Теперь можно определить понятие оптимального стабилизирующего управления, как функции переменных состояния и времени, при которых на движение системы (25), возмущенного произвольными начальными отклонениями (2) и (3), показатель качества (29) принимает наименьшее значение.

Примечание. Стабилизирующее управление реализуется регулятором, который является сложным динамическим устройством, состоящим обычно из трех компонент:

- измерительных органов,

- устройств реализации алгоритма управления,

- исполнительных органов.

Уравнения (25) – это уравнения физического объекта вместе с измерительными и исполнительными устройствами регулятора. При этом

Δx(t) – выход измерительного устройства, а ΔU(t) - вход исполнительного устройства. Уравнение (30) описывает устройство реализации алгоритма управления.

Для упрощения терминологии будем называть уравнениями объекта уравнения (25) и (24) известной (неизменной) части системы, состоящей из объекта и элементов регулятора. Уравнением регулятора будем называть уравнение (30), описывающее неизвестную (подлежащую определению) часть системы, состоящую лишь из устройства реализации алгоритма управления.

6. Рассмотрим обобщенную структурную схему реализаций программного и стабилизирующего управлений, на которой объект управления описывается уравнением (1), а регулятор реализует стабилизирующее управление (30).

Объект вместе с задатчиками программного управления и движения образуют систему программного управления, а объект вместе с регулятором – систему стабилизации программного управления.

Различие способа функционирования системы программного управления и системы стабилизации состоит в следующем.

1. Для первой начальные условия (2) известны до начала проектирования, а для второй они неизвестны, известно лишь что они находятся в пределах, установленных неравенством (22).

2. Для первой управление является главной функцией времени, а для второй – функцией измеряемых переменных. Следовательно, для первой управление осуществляется по разомкнутому принципу, а для второй – по принципу обратной связи.

3. Эффективность системы программного управления оценивается интегралом (4), в котором функция 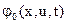определяется физической природой объекта управления. В системе стабилизации критерий (29) часто не связан с физической природой объекта управления, а его коэффициент q определяется, исходя из инженерных требований (времени переходного процесса от истинного движения к программному, перерегулирования при этом движении, установившейся ошибки осуществления программного движения). Однако в теории автоматического управления критерий (29) полагают заданным, оставляя вопросы выбора коэффициентов q и γ за пределами этой теории.

4. При построении стабилизирующего управления (30) обычно используют уравнения первого приближения (25). Использование уравнений первого приближения при построении программного управления, как правило, недопустимо.