Свойства преобразования Лапласа
Интеграл Фурье
Применение преобразования Лапласа
1. В предыдущем разделе использовался оператор дифференцирования 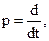 с помощью которого дифференциальное уравнение динамики линейной системы преобразовалось в алгебраическое уравнение того же порядка. Использование этого оператора носило чисто символический характер. Преобразование Лапласа раскрывает математический и физический смысл этого оператора и устанавливает важную связь между передаточной и весовой функциями линейной системы. Однако, прежде чем рассматривать преобразование Лапласа, необходимо рассмотреть преобразование Фурье, которое лежит в основе преобразования Лапласа.
с помощью которого дифференциальное уравнение динамики линейной системы преобразовалось в алгебраическое уравнение того же порядка. Использование этого оператора носило чисто символический характер. Преобразование Лапласа раскрывает математический и физический смысл этого оператора и устанавливает важную связь между передаточной и весовой функциями линейной системы. Однако, прежде чем рассматривать преобразование Лапласа, необходимо рассмотреть преобразование Фурье, которое лежит в основе преобразования Лапласа.
Любой сигнал можно представить в виде временной функции ¦(t) и в виде частотной функции F(w). Связь между этими двумя формами представления устанавливает преобразование Фурье. Прямое преобразование Фурье позволяет найти F(w), если известна ¦(t). Обратное п.Ф. позволяет восстановить ¦(t) по известному спектру F(w). Это отображается следующим образом:
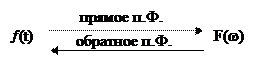 |
В начале рассмотрим п.Ф. периодической функции.
Любую периодическую функцию ¦(t) можно представить в виде синусо-косинусного ряда:
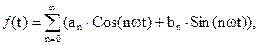 (1)
(1)
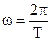 , где Т – период функции, w - круговая частота.
, где Т – период функции, w - круговая частота.
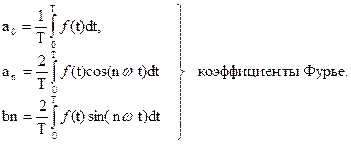
Функцию ¦(t) можно представить в виде синусного ряда 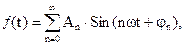 где
где 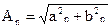 ,
, 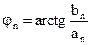 , An – амплитуда n-ой гармоники, jn – фаза n-ой гармоники.
, An – амплитуда n-ой гармоники, jn – фаза n-ой гармоники.
Если использовать преобразование Эйлера:
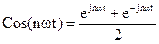 ,
, 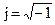 ,
, 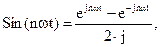 то выражение (1) можно представить в экспоненциональной форме:
то выражение (1) можно представить в экспоненциональной форме:
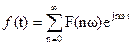 – обратное преобразование Фурье.
– обратное преобразование Фурье.
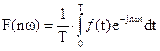 – прямое преобразование Фурье.
– прямое преобразование Фурье.
2. Для периодического сигнала частотный спектр является линейчатым. Если функция непериодическая, то тогда преобразования нужно будет вычислять при T®¥. Непериодическую функцию можно считать периодической, если T®¥, Dw®0, тогда
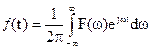 , интеграл Фурье.
, интеграл Фурье.
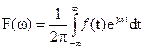 (2)
(2)
Спектр непрерывной функции представляет собой сплошную (непрерывную) функцию. Эти два интеграла существуют, если выполняется условие:
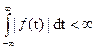 (3)
(3)
Широко используемые в теории управления функции (¦(t)=1(t), ¦(t)=kt и др.) не удовлетворяют этому условию.
3. Поскольку для этих функций интегралы Фурье не существуют, поэтому преобразование Фурье применять не имеет смысла. Рассмотрим класс функций ¦(t)=Me-at, где M>0, a>0, для которых условие (3) выполняется. Эти функции называются экспоненциальными, они достаточно хорошо отображают большинство процессов, совершающихся в природе. Экспоненциальная функция с параметром a<0 отображает затухающий (устойчивый) процесс, причем степень затухания зависит от величины a. Функции, для которых a=0 являются незатухающими, а для a>0 являются неограниченными функциями на полуоси t>0. Обе эти функции соответствуют условно устойчивым (a=0) и неустойчивым (a>0) процессам, которые на практике встечаются крайне редко. Кроме того, рассматриваются экспоненциальные функции, которые равны нулю для t<0. Такие функции удобно использовать для изучения переходных режимов (момент t=0 соответствует моменту времени, при котором начинается возмущения, порождающие переходной процесс).
Расмотрим функцию  . В соответствии с выражением (2) найдем её спектр для t³0:
. В соответствии с выражением (2) найдем её спектр для t³0: 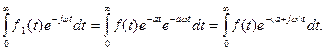 Обозначим через p=a+jw. Тогда
Обозначим через p=a+jw. Тогда 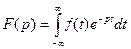 - интеграл Лапласа.
- интеграл Лапласа.
Функцию ¦(t) называют оригиналом, а F(p) – изображением. Показатель p называется комплексной частотой.
Обратное преобразование Лапласа 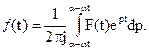
На практике используют преобразование Карсона-Лапласа:
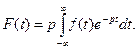 (4)
(4)
Это преобразование позволяет получить в более простой форме изображения некоторых функций. Проведем примеры вычисления преобразования Карсона-Лапласа.
Пример 1.
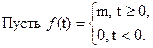
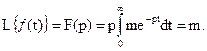
Пример 2. ¦(t)=e-at. 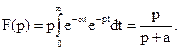 Отметим, что в своей практической работе инженерам нет необходимости вычислять изображения по оригиналу, используя формулу (4). В литературе по теории управления имеются таблицы изображений большинства наиболее употребляемых функций.
Отметим, что в своей практической работе инженерам нет необходимости вычислять изображения по оригиналу, используя формулу (4). В литературе по теории управления имеются таблицы изображений большинства наиболее употребляемых функций.
4. Приведем без доказательства некоторые основные свойства преобразования Лапласа.
1. Пусть 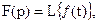 тогда
тогда 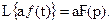
Пусть 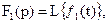 и
и 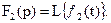
Тогда 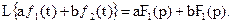
3. Свойство задержки (смещения).
Пусть 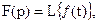
Тогда 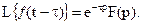
4. Свойство дифференцирования.
Пусть 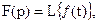
Тогда 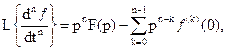 где
где 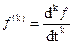
Пример. 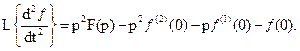
5. Свойство свертки.
Пусть 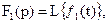 и
и 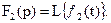
Тогда 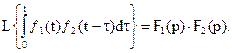
В пользе приведенных свойств нетрудно убедиться, рассмотрев операторный способ преобразования линей
ного дифференциального уравнения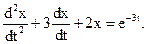 Для упрощения примем
Для упрощения примем 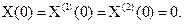 Тогда в силу свойств 1,2, и 4
Тогда в силу свойств 1,2, и 4
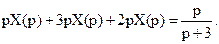
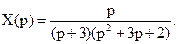
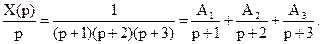
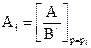
Используя таблицы пребразований Лапласа можно по изображению X(p) получить оригинал X(t), при упомянутых начальных условиях.
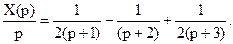
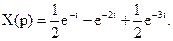
5. В предыдущем разделе было упомянуто о возможностях весовой функции линейной системы.
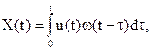 где u(t), X(t) – значение входа и выхода линейной системы,
где u(t), X(t) – значение входа и выхода линейной системы,
w(t) – весовая функция системы.
X(t) – представляет свертку функций u(t) и w(t).
Воспользуемся ранее приведенным свойством преобразования Лапласа (свойство свёртки).
Если 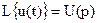 и
и 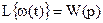 , то
, то 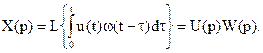
Отсюда
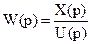 (5).
(5).
Выражение (5) мы назвали передаточной функцией в операторной форме. Теперь можно дать более глубокое толкование выражения (5):
передаточная функция системы W(p) есть отношение изображения выходной величины этой системы к изображению входной величины при условии, что система в начальный момент времени находилась в покое.
Кроме того, можно сделать ещё один очень важный вывод: передаточная функция W(p) есть преобразование Лапласа импульсной (весовой) переходной функции линейной системы.
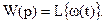
 2014-02-02
2014-02-02 1052
1052
