Разностные уравнения
Последовательности дискретных сигналов
Линейные системы с постоянными параметрами
2. ЛПП – системы
1. Последовательность дискретных сигналов.
Математики дискретные сигналы представляют в виде непрерывной последовательности чисел:
{h(n)}, {h(nT)}, h(n), h(nT), N1 £ n £ N2
При графическом изображении последовательностей используются два способа.
а) в виде отрезка в точке h0
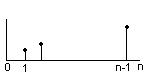
б) в виде огибающей
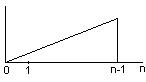
Наиболее важные последовательности, используемые при ЦОС:
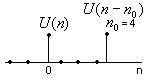
1) Цифровой единичный импульс (отсчет)
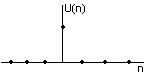
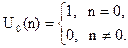
2) Единичный импульс, задержанный на n0 отсчетов
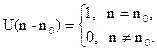
3) 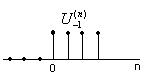 Единичный скачок
Единичный скачок
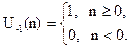
Единичный скачок связан с единичным импульсом соотношением:
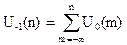
4) Убывающая экспонента
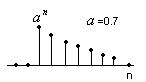
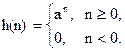
5) Косинусоида
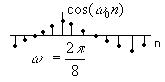
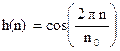 для всех n.
для всех n.
6) Комплексная экспонента:
ejwn = cos(wn) + jsin(wn).
Для ее изображения нужны разделенные графики для действительной и мнимой частей.
7) Произвольная последовательность
a(0), a(1), a(2),…,a(n), где a(n) – величина n-го элемента
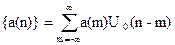
 2014-02-02
2014-02-02 630
630







