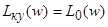 ;
;
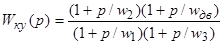 ;
;
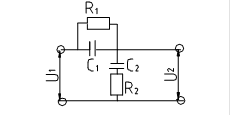
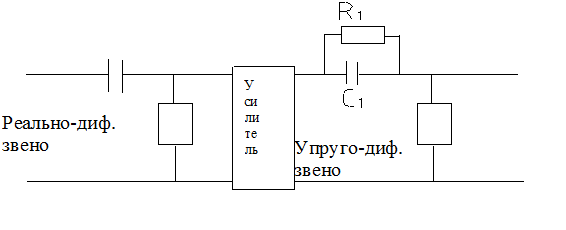
Параллельная коррекция
По 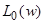 восстанавливаем
восстанавливаем 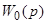 ;
;
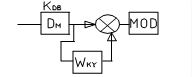
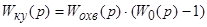 ;
;
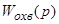 -звенья, охваченные параллельной коррекцией;
-звенья, охваченные параллельной коррекцией;
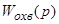 =1;
=1;
 |
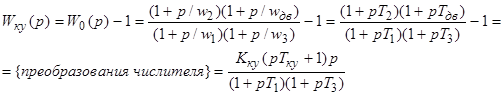
 41. Дискретные системы автоматического управления. Типы дискретизации. Структурные схемы импульсных систем.
41. Дискретные системы автоматического управления. Типы дискретизации. Структурные схемы импульсных систем.
Вдискретных системах сигналы дискретны. Для дискретных сигналов характерны скачки. Для любой точки: предел слева не равен пределу справа.
Причины дискретизации:
1. 1. Сигнал на входе дискретный.
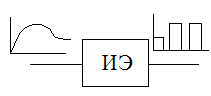
2. 2. 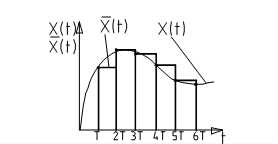 Существует элемент, осуществляющий дискретизацию.(ИЭ)
Существует элемент, осуществляющий дискретизацию.(ИЭ)
Большинство систем относится к п.2.
Опр: Преобразование непрерывного сигнала в дискретный наз. квантованием.
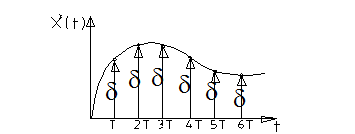
1. 1. Квантование по времени.
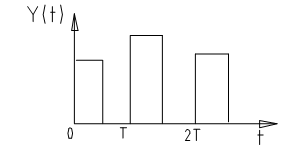
Фиксируем моменты времени T1...T5 и фиксируем ординаты сигнала. (Т-период квантования, интервал дискретизации).
Системы, в которых осуществляется квантование по времени, наз. импульсными системами.
Пример: кинопленка.
2. 2. 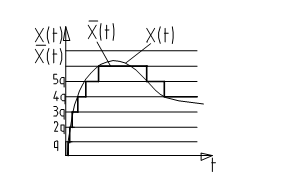 Квантование по уровню.
Квантование по уровню.
Фиксируем уровень(ординату), q-квант по уровню.
Системы, в которых осуществляется квантование по уровню, наз. релейными системами.(класс нелинейных систем)
Пример: цифровые весы, вольтметры, амперметры...
3. 3. 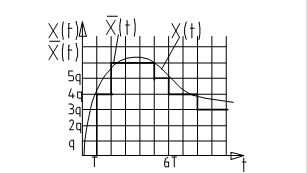 Квантование по уровню и по времени (комбинированный).
Квантование по уровню и по времени (комбинированный).
Округление до ближайшего кванта.
Системы в которых осуществляется квантование по уровню и по времени наз. цифровыми системами (относятся к нелинейным системам).
Пример: любая система, подключенная к ЭВМ.
Форма импульса, вырабатываемая импульсным элементом может быть разная: прямоугольная, треугольная, экспоненциальная и т.д.
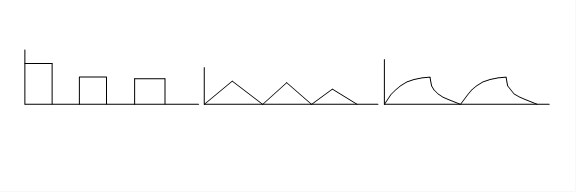 |
В импульсном элементе (ИЭ) вырабатывается последовательность выходных импульсов, зависящая от ординат входного сигнала в дискретные моменты времени.
Зависимость какого-либо параметра импульса от ординаты входного сигнала наз. модуляцией.
Существуют различные виды модуляций:
- Амплитудно-импульсная модуляция (АИМ), зависимость от амплитуды.
- Широтно-импульсная модуляция (ШИМ).
- Время-импульсная модуляция.
· · Частотно-импульсная модуляция (ЧИМ). 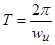 -меняется частота следования импульсов.(чем больше амплитуда, тем чаще идут импульсы)
-меняется частота следования импульсов.(чем больше амплитуда, тем чаще идут импульсы)
· · Фазо-импульсная модуляция (ФИМ). При ФИМ меняется фаза импульса.
Мы будем рассматривать системы с АИМ-линейные импульсные системы.
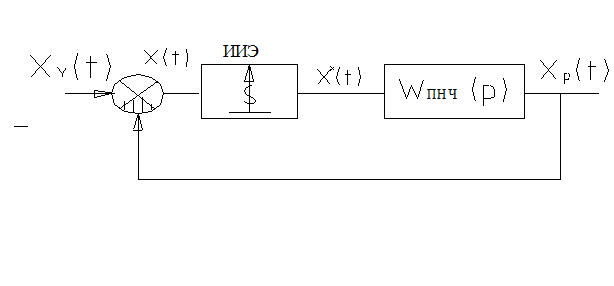
Структурная схема линейных импульсных систем.
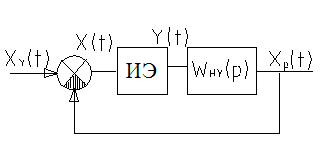
 -управляющий непрерывный сигнал;
-управляющий непрерывный сигнал;
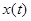 -сигнал ошибки или отклонения (непрерывный);
-сигнал ошибки или отклонения (непрерывный);
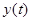 -последовательность импульсов на выходе импульсного элемента;
-последовательность импульсов на выходе импульсного элемента;
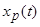 -регулируемый сигнал (непрерывный);
-регулируемый сигнал (непрерывный);
Каждый импульс можно рассматривать, как реакцию системы на 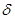 -функцию.
-функцию.
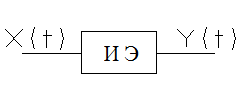
Можем заменить ИЭ идеальным импульсным элементом (ИИЭ).
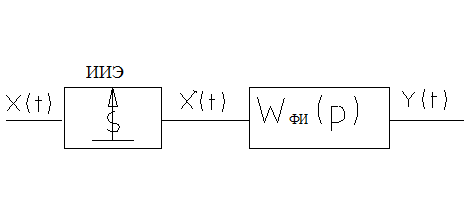
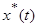 -последовательность
-последовательность 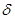 -функций, модулированная ординатами входного сигнала
-функций, модулированная ординатами входного сигнала 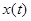 в дискретные моменты времени.
в дискретные моменты времени.
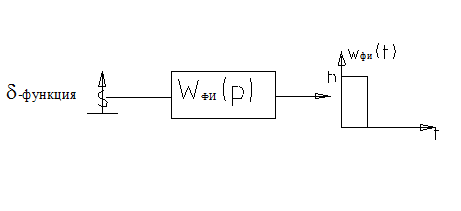
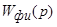 -передаточная функция формирователя импульсов (вид зависит от формы вырвбатываемого импульса).
-передаточная функция формирователя импульсов (вид зависит от формы вырвбатываемого импульса).
Реакция системы на 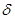 -функцию является весовая функция.
-функцию является весовая функция.
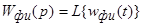 ;
;
Пример определения передаточной функции Wфи(p):
Прямоугольный импульс.
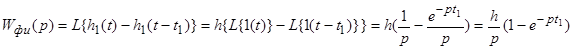 ;
;
Треугольный импульс.
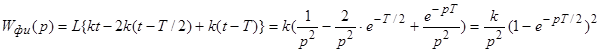 ;
;
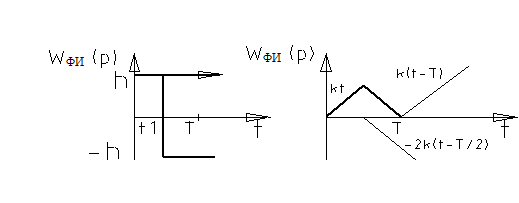
Перерисуем структурную схему:
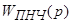 -приведенная непрерывная часть системы;
-приведенная непрерывная часть системы;
 |
Окончательно:
42. Понятие решетчатой и модулированной функций. Дискретное преобразование Лапласа.
Математическим аппаратом для исследования импульсных систем является дискретное преобразование Лапласа.
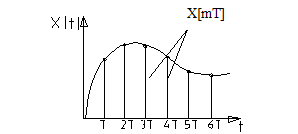
х[mT]-решетчатая функция, состоит из ординат;
Модулированный сигнал (последовательность 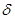 -функций, модулированная ординатами входного сигнала в дискретные моменты времени).
-функций, модулированная ординатами входного сигнала в дискретные моменты времени).
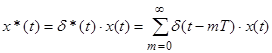 ;
;

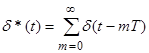 ;
;
Сигнал 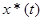 -реально существующий сигнал;
-реально существующий сигнал;

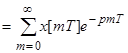 ;
;
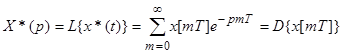 ;
;
D-дискретное преобразование Лапласа.
43. Свойства дискретного преобразования Лапласа.
1. 1. Линейность.
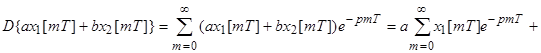
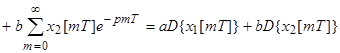 ;
;
2. 2. (Преобразование Лапласа от запаздывающего аргумента). Смещение по времени.
а) Запаздывание на S тактов.
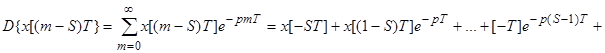
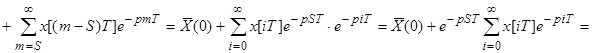
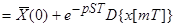 ; где i=m-S.
; где i=m-S.
При нулевых начальных условиях (ННУ):
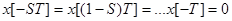 ;
;
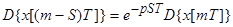 ;
;
б) Упреждение m+S=i; m=i-S;
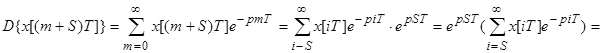
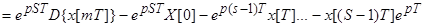 ; при не ННУ
; при не ННУ
При ННУ:
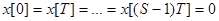 ;
;
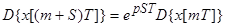 ;
;
3. 3. Преобразование Лапласа от конечных разностей.
Первая разность - 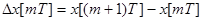 ;
;
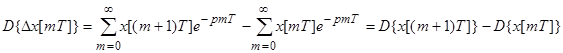 ;
;
При ННУ:
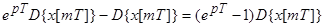 ;
;
Непрерывные системы-p;
Дискретные системы-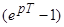 ;
;
Вторая разность-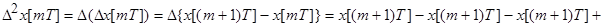
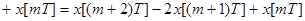 ;
;
При ННУ:
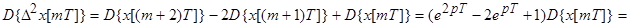
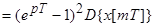 ;
;
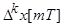 -к-ая разность-
-к-ая разность-
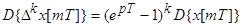 ;
;
4. 4. Преобразование от суммы:
Найдем первую разность.
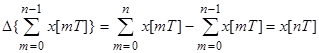 ;
;
Возьмем преобразования Лапласа от правой и левой части выражения.
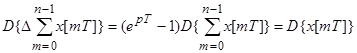 ;
;
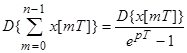 ;
;
5. 5. Теорема о предельном значении.
По анологии с непрерывными системами: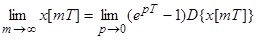 ;
;
6. 6. Сумма ординат решетчатой функции.
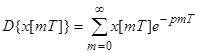 ;
;
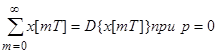 ;
;
44. Дискретные передаточные функции. Дискретные типовые сигналы и их изображение.
Для непрерывных систем: 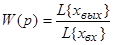 при ННУ;
при ННУ;
 |
Для дискретной системы:
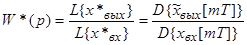 при ННУ;
при ННУ;
1. 1. Дельта-функция.
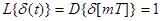 ;
;
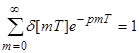 ;
;
2. 2. Единичная ступенчатая функция.(1(t))
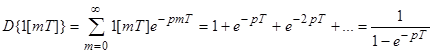 ;
;
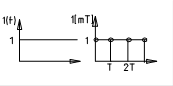 Это бесконечно убывающая прогрессия:
Это бесконечно убывающая прогрессия: 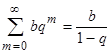 ;
;
3. 3. Линейно возрастающая функция.
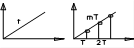
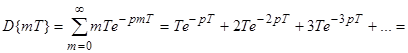
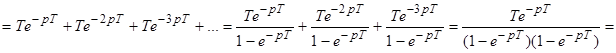
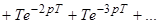
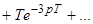
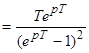 ;
;
4. 4. Экспонента.
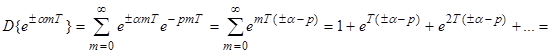
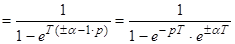 ;
;
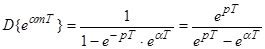 ;
;
 2014-02-02
2014-02-02 706
706







