Частотные критерии устойчивости

1 2 3 4 5 6 7

Алгебраические критерии устойчивости

Условия устойчивости по первому приближению

Асимптотическая устойчивость, устойчивость в целом

Определение устойчивости невозмущенного движения по Ляпунову

Уравнение возмущенного движения

Возмущенное и невозмущенное движение

Задача Коши

Устойчивость линейных систем

Тогда

G_посл(z) = G₁(z)G₂(z) = (0,2 + z^-1+ z^-2) / (1 - 0,3z^-1),

G_пар(z) = G₁(z) + G₂(z) = 1 / (1-0,3z^-1) + 0,2 + z^-1+ z^-2,

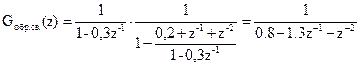1. Основоположниками теории устойчивости являются русский ученый Александр Михайлович Ляпунов (1857-1918) и французский ученый Анри Пуанкаре (1856-1912). Одним из создателей современной теории устойчивости является Николай Гурьевич Четаев (1902-1959), профессор КАИ, глава Казанской школы по теории устойчивости движения. Запишем уравнение динамики системы 1-го порядка.

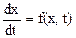(1)

С начальными условиями

x(t₀) = x₀ (2)

Здесь функция f(x,t) дифференцируема по аргументу t на интервале [t₀,¥]. Выражения (1), (2) называют задачей Коши. Т.к. задача теории устойчивости в форме Коши впервые возникла в механике, то переменную t принято интерпретировать как время tÎI=[t₀,+¥], а искомую функцию x(t) – как движение точки в зависимости от времени. Пусть задача Коши удовлетворяет условиям теоремы существования и единственности. Тогда через каждую точку (x₀,t₀) области единственности решений проходит только одна интегральная кривая. Если начальные данные (x₀,t₀) изменяются, то изменяется и решение. Если математической моделью системы является задачей Коши и малые изменения начальных данных приводит к существенному изменению решения, то такой моделью нельзя пользоваться, поскольку начальные данные получают из опыта, т.е. путем измерений, а изменения не могут быть абсолютно точными. Поэтому в качестве математической модели системы пригодны лишь та задача Коши, которая устойчива к малым изменениям начальных данных.

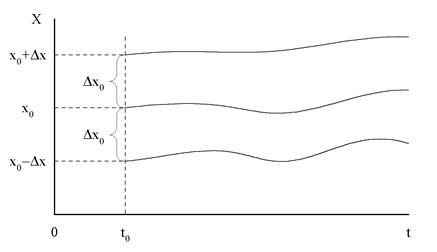
Рис. 1. Графическое представление задачи Коши.

2. Некоторое вполне определенное значение движение системы, подлежащее исследованию на устойчивость, называется невозмущенным движением. Невозмущенному движению системы отвечает определенное частное решение уравнения (1), которое представлено на рис. 1. в виде интегральной кривой x(t,t₀). Изменим условия (2), дав начальному значению x₀ переменной x небольшое по модулю приращение, которое называется возмущением. Тогда движение системы (1) с измененным начальным условиям x₀+Dx₀будет называться возмущенным в положительном направлении движением. Этому движению будет соответствовать интегральная кривая x(t,t₀,Dx₀) на рис. 1. Аналогично движение системы(1) с измененным начальным условием x₀-Dx₀будет называться возмущенным в отрицательном направлении движением (кривая x(t,t₀,-Dx₀) на рис. 1.).