Тогда
x*(t)= x(t)+ Dx(t) (3)
Внесем значение (3) в дифференциальное уравнение (1). Получим
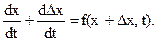
Разложим правую часть уравнения в ряд Тейлора по степеням Dx
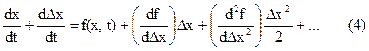
Обозначим через

Тогда выражение (4) (при условии 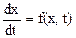 ) можно записать в виде:
) можно записать в виде:
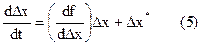
Уравнение (5) называется дифференциальным уравнением возмущенного движения. Если в этом уравнении отбросить член Dx*, то полученное при этом уравнение
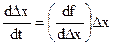 (6)
(6)
называется уравнением первого приближения.
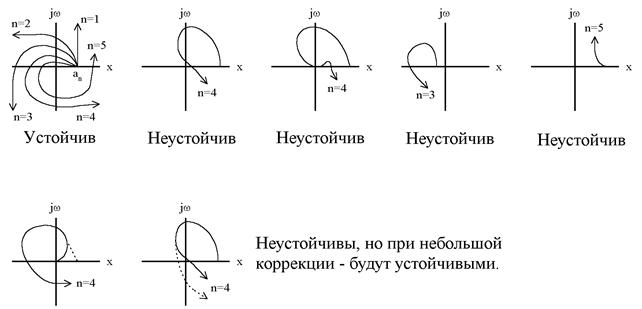
Уравнение первого приближения во многих случаях дает верный ответ на вопрос об устойчивости движения, но отметим, что это соблюдается не всегда. Введем обозначения
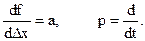
Тогда уравнение (6) приводится к виду:
(p+a)Dx = 0 (7)
Выражение в скобках p+a называется характеристическим многочленом системы. С учетом выражения (3) траектории возмущенного и невозмущенного движения удобно представлять так, ка на рис.2.
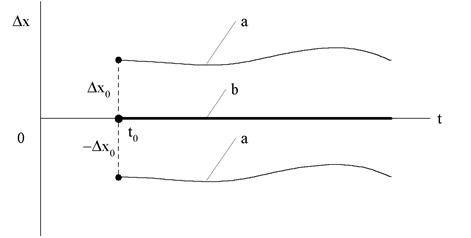
Рис.2. Графическое представление траекторий возмущенного (а) и невозмущенного движений системы (b).
Возмущения ± Dx0 действуют в момент времени t0, при этом траектория невозмущенного движения совпадает с осью абсцисс (осью времени).
4. Как определить устойчиво ли невозмущенное движение системы? Ответ на этот вопрос дал в 1892 г. А М. Ляпунов. Он предложил в произвольный момент времени t0 ввести в невозмущенное движение возмущенное Dx0 (например, в положительном направлении) и по характеру возмущенного движения Dx(t) системы для любого момента времени t> t0, судить об устойчивости невозмущенного движения. Приведем определение устойчивости по Ляпунову. Невозмущенное движение называется устойчивым по отношению к переменным Dx, если при произвольно выбранном числе e>0,как бы мало оно не было, можно выбрать другое такое же число d(e)>0, что при всяких возмущениях Dx0, удовлетворяющих условию Dx0£d и при любом t ³ t0 будет выполняться неравенство Dx<e. В противном случае движение не устойчиво. Геометрическая интерпретация определения приведена на рис. 3.
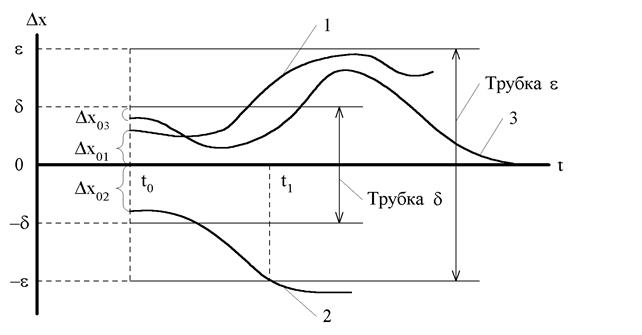
Рис.3. Графическое представление определения устойчивости.
Зону образованную прямыми ±d параллельными оси называют d–трубкой, аналогичную зону образованную прямыми ±e, называют e–трубкой. Возмущенное движение 1 будет устойчивым, т.к. оно не выходит за пределы e–трубки, а возмущенное движение 2 будет неустойчивым, т.к. в момент времени t1 > t0 оно выходит за пределы e–трубки. При этом в обоих случаях возмущения Dx01 и Dx02 не выходит за пределы d–трубки.
5. Устойчивое движение по Ляпунову будет называться асимптотическим устойчивым, если "t > t0,
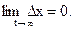
Траектория возмущенного движения 3 на рис.3. не только не выходит за пределы e–трубки, но и при достаточно большом t асимптотически стремиться к оси t. Поэтому система, получающая в момент времени t0 возмущение Dx03 и имеющая для всех t > t0 траекторию 3 возмущенного движения (рис. 3.), будет асимптотически устойчивой.
Если система асимптотически устойчива при достаточно больших возмущениях, то она называется устойчивой в целом.

Рис. 4. Примеры устойчивых и неустойчивых систем.
На рис.4. (a) приведен пример маятника, представляющего собой тело, укрепленное на стержне, массой которого можно пренебречь, точка 0 является неподвижной точкой подвеса маятника. Если маятника находится в положении 1, то наибольшее возмущение Dx01 выведет из состояния равновесия. Следовательно, маятник в положении 1 является не устойчивой системой. Если маятник, находящийся в положении 2, отклонить на угол Dx02 и пренебречь силой трения в опоре и сопротивлением воздуха, то маятник будет совершать устойчивые незатухающие колебания относительно положения 2. Такая система будет устойчивой. Если учесть трение в опоре и сопротивление воздуха, то через достаточно большое время маятник вернется в положение 2, и в этом случае он представляет собой асимптотически устойчивую систему или систему устойчивую в целом. Аналогично шары, находящиеся на гладких поверхностях (b) и (c), будут представлять собой соответственно неустойчивую и асимптотически устойчивую систему.
6. Ранее рассматривалась система (1), описываемая дифференциальным уравнением 1-го порядка. Если рассмотреть общий случай, когда исследуемая на устойчивость система описывается дифференциальным уравнением n-го порядка, то уравнение первого приближения можно записать следующим образом:
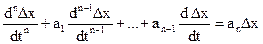 , (8)
, (8)
где a1,..an –постоянные коэффициенты, причем 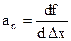 .
.
Характеристический многочлен системы будет иметь вид:
G(p) = a0pn + a1pn-1 +…+ an-1p + … + an,
а характеристическое уравнение:
a0pn + a1pn-1 + … + an-1p + … + an = 0 (9)
имеет корни (полюса) 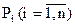 .
.
Эти корни в общем случае являются комплексными Pi = ai + jwi, т.е. содержат вещественную и мнимую части. Если корень имеет отрицательную вещественную часть, т.е. ai < 0, то он называется левым, т.к. точка, изображающая его положение на комплексной плоскости, располагается слева от мнимой оси (рис. 5.).
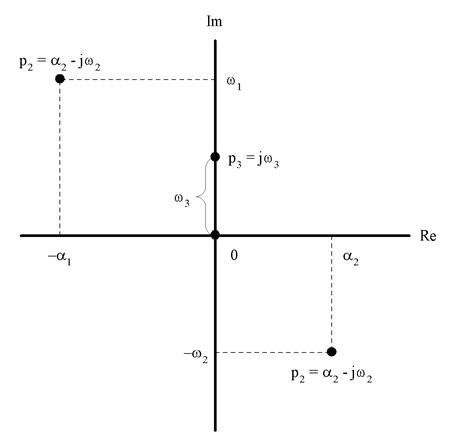
Рис. 5. Расположение корней характеристического уравнения на комплексной плоскости (Re – вещественная ось, Im – мнимая ось).
Корень p1 будет левым, корень p2 будет правым, а p3, расположенный на мнимой оси (a3 = 0), называется нейтральным.
Пример 1. Характеристическое уравнение:
p2 - 4p + 13 = 0;
 .
.
Оба корня являются правыми.
Теорема 1. Если вещественные части всех корней pi характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво.
Теорема 2. Если среди корней pi характеристического уравнения первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение устойчиво.
На основании этих теорем, чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни характеристического уравнения были левыми.
Необходимым условием устойчивости для систем любого порядка является положительность всех коэффициентов характеристического уравнения.
Для систем 1-го и 2-го порядков необходимое условие устойчивости является и достаточным условием устойчивости. Система, характеристическое уравнение которой приведено в примере 1, является неустойчивой.
Пример 2. Характеристическое уравнение системы имеет вид:
p2 - 4p + 13 = 0;
p1,2 = -2 ± 3j.
Поскольку оба корня уравнения левые, то система будет асимптотически устойчивой.
Пример 3. Характеристическое уравнение системы имеет вид:
p2 - 2p = 0;
p1 = 0, p2 = -2.
Корень p1 –нейтральный, корень p2 –левый.
Поэтому система будет условно устойчивой, аналогично маятнику находящемуся в состоянии незатухающих колебаний относительно положения II (рис. 4. (а)).
Если характеристическое уравнение исследуемой цифровой системы имеет вид:
G(z) = anzn + an-1zn-1 +…+a0
То необходимо и достаточным условием устойчивости системы является то, что все полюса по модулю должны быть меньше единицы. Другими словами, все корни G(z) должны лежать внутри круга единичного радиуса.
Пример: Передаточная функция замкнутой цифровой системы:
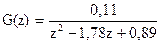
Определить устойчивость системы.
Характеристическое уравнение системы:
z2 - 1,78p + 0,89 = 0
Корни (полюса):
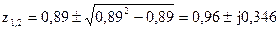
Модуль полюсов:
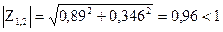
Критерий устойчивости – это правила, которые позволяют определять устойчивость системы без вычисления корней характеристического уравнения. Все критерии делятся на:
- алгебраические;
- частотные.
7. Алгебраические критерии устойчивости позволяют судить об устойчивости системы по коэффициентам характеристического уравнения.
Критерий Раусса (англ. 1877г.).
G(p) = a0pn + a1pn-1 + … + an
Составляется таблица:
| Коэффициент, ri | Строка, i | Столбец, j | |||
| - | a0 = c11 | a2 = c21 | a4 = c31 | a6 = | |
| - | a1 = c12 | a3 = c22 | a5 = c32 | a7 = | |
| r3 = a0 / a1 | с13 = | ||||
| r4 = c11 / c13 | с14 = | ||||
| r5 = c13 / c14 | |||||
| … | |||||
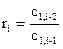 | i | c1i = c2,i-2 – ric2,i-1 |
Для того, чтобы система была устойчива необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Раусса имели один и тот же знак.
Пример. Пусть:
G(p) = p6 + 6p5 + 21p4 + 44p3 + 62p2 + 52p + 100 = 0.
Составим таблицу Раусса:
| Коэффициент, ri | Строка i | Столбец, j | |||
| - | a0 = 1 | a2 = 21 | a4 = 62 | a6 = 10 | |
| - | a1 = 6 | a3 = 44 | a5 = 52 | a7 = 0 | |
| r3 = a0 / a1 = 1/6 = = 0,167 | с13=21-‑0,167×44= =13,65 | с23=62-‑0,167×52= =53,3 | с33 = 100 | ||
| r4 = a1/c13 = 6/13,65 = = 0,44 | с14=44 -‑0,44×53,3= =20,6 | с24=52 -‑0,44×100= =8 | |||
| r5 = c13 / c14 = = 13,65/20,6 = 0,66 | с15 = 48 | с25 = 100 | |||
| r6 = c14 / c15 = = 20,6/48 = 0,43 | с16 = -35 | ||||
| r7 = c15 / c16 = = 48/‑35 = -1,37 | с17=100‑ ‑(‑1,37)×0= =100 |
Имеется две переменные знака коэффициента первого столбца. Следовательно, система неустойчива, а уравнение G(p) имеет два правых корня.
В основе частотного критерия устойчивости лежит принцип аргумента: Изменение (приращение) аргумента G(jw) при изменение w от -¥ до ¥ равно разности между числом левых и правых корней уравнения G(p) = 0, умноженной на p.

где m – число правых корней,
n – число левых корней.
Критерий Михайлова (1938).
Система устойчива, если годограф обходит последовательно n квадрантов в положительном направлении, где n – порядок характеристического уравненния G(p).
Для цифровых систем критерий, эквивалентный критерию Рауса-Гарвица, был предложен Джури. Чтобы определить, все ли корни многочлена
G(z) = a0zn + a1zn-1 + … + an
находятся внутри единичного круга, составляют следующую таблицу:
| a0 | a1 | ... | an-1 | an | 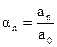 |
| an | an-1 | a1 | a0 | ||
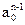 | 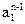 | 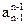 | 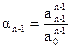 | ||
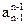 | 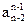 | 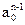 | |||
| .......... | |||||
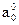 |
где:
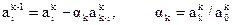
Первая и вторая строки - это коэффициенты характеристического многочлена в прямом и обратном порядке. Третья строка получается умножением второй строки на an=an/a0 и вычитанием произведения из первой строки, т.о. последний элемент в третьей строке равен 0. Четвертая строка - это третья, записанная в обратном порядке. Схема повторяется до (2n+1) строки. Последняя строка состоит только из одного элемента.
Критерий Джури.
Если a0>0, то вcе корни многочлена лежат внутри единичного круга тогда и только тогда, когда все 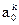 , k = 0, 1, 2,..., n-1 положительны. Если нет
, k = 0, 1, 2,..., n-1 положительны. Если нет 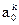 равных нулю, то количество отрицательных
равных нулю, то количество отрицательных 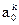 равно количеству корней вне единичного круга.
равно количеству корней вне единичного круга.
Пример. Задано характеристическое уравнение системы:
z2 + a1z + a2 = 0
Таблица Джури имеет следующий вид:
| a1 | a2 | 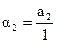 | ||
| a2 | a1 | |||
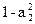 | a1(1-a2) | 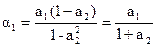 | ||
| a1(1-a2) | 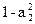 | |||
 |
Все корни характеристического уравнения находятся внутри единичной окружности, если:
 ,
,
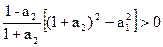 .
.
Отсюда условия устойчивости определяютсякак:
a2 < 1
a2 > -1 + a1
a2 > -1 - a1

Область устойчивости для исследуемого уравнения как функция коэффициентов a1 и a2 может быть представлена графически.
 2014-02-02
2014-02-02 2020
2020
