2014-02-02
926
Лекция №10
Контрольные вопросы
1. Какова размерность векторного потенциала?
2. Каково соотношение между векторным потенциалом и вектором индукции?
3. Что является решением уравнения Пуассона?
4. Каковы граничные условия для уравнения Лапласа?
Индуктивность. Энергия магнитного поля.
1. Выражение магнитного потока через векторный потенциал.
2. Расчёт индуктивности и взаимной индуктивности.
3. Расчёт индуктивности двухпроводной линии.
4. Энергия магнитного поля, силы в магнитном поле.
Краткое содержание лекции
Если магнитный потенциал создаётся вектором намагниченности, то его величина равна:
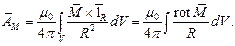
Закон Био-Савара можно вывести из формулы для векторного потенциала. Если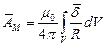 
, а 
, то
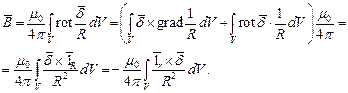
Используя теорему Стокса, можно выразить магнитный поток через векторный потенциал:
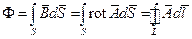 | (1) |
Расчёт индуктивности производится в следующей последовательности. Рассчитывается магнитный поток и берётся отношение потокосцепления к току в контуре:
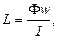
здесь I – ток; w – число витков.
При расчёте взаимной индуктивности находится поток, наведённый соседним контуром в некотором контуре, а затем находятся отношения:
;
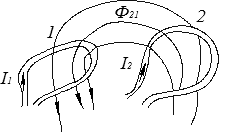
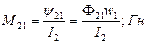
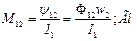
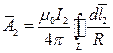а согласно (1)
; 
; 
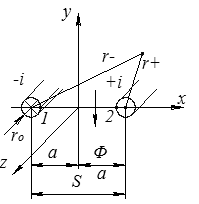
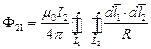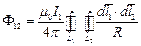То есть расчёт индуктивности и взаимной индуктивности сводится к расчёту потока, сцеплённого с данным контуром.
Векторный потенциал двухпроводной линии в любой точке, отстоящей на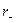 
от левого провода и 
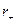от правого провода, выражается формулой:
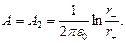 | (2) |
Магнитный поток, сцеплённый с каким-либо контуром, согласно (1) равен:
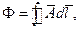
поэтому, пользуясь формулой (2), легко найти поток, проходящий по воздуху между двумя проводами с радиусами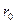 
на расстоянии 
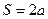между их осями.
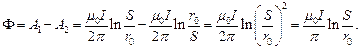
Индуктивность будет равной:
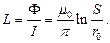
Напомним, что ёмкость двухпроводной линии равна:
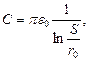
тогда
,
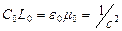где c2 – квадрат скорости света, как исследовало ожидать, поскольку скорость распространения электромагнитных волн равна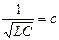 
.
Индуктивность кабеля.
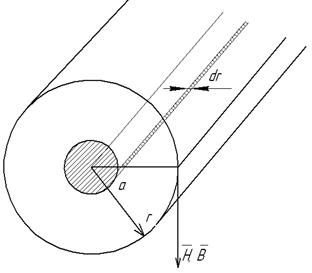
Согласно закону полного тока:
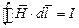или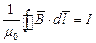 
Внутри провода по сечению πr2 протекает ток, равный:
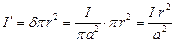
Тогда:
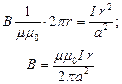
По полосе шириной dr проходит поток:
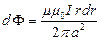
Внутреннее потокосцепление:
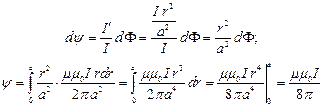
Отсюда индуктивность равна:
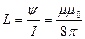
Если μ = 1000, то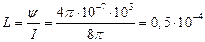 
Гн.
Энергия магнитного поля
Энергия магнитного поля, занимаемого объём V равна:
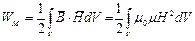 | (3) |
Пользоваться формулой (3) не всегда удобно, так как приходится интегрировать по объёму, который иногда трудно определить. Поэтому, если поле создаётся токами плотностью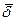 
целесообразно использовать формулу, получаемую следующим путём:
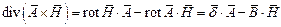
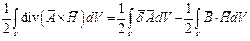
или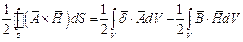 
.
Первый интеграл равен нулю, так как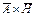 
убывает, как 
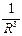, а площадь растёт как R2. Поэтому окончательно получаем:
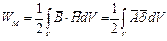 | (4) |
Интеграл (4) вычислить проще, так как интегрирование производится по объёму, в котором имеется вектор .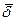
Сила в магнитном поле определяется как:
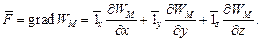
Правило Максвелла.
Во всех случаях, определяя силы, появляющиеся под действием магнитного поля, можно руководствоваться следующим правилом: провода с током и те другие тела, находящиеся в магнитном поле, всегда стремятся к перемещению, при котором увеличивается магнитный поток или полное магнитное потокосцепление.
В намагниченной среде электрический момент единицы объёма равен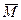 
, поэтому действующая на эту среду объёмная сила:
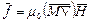
Когда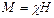 
,
Применяя известное преобразование векторного анализа
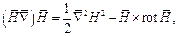
находим, что в безвихревом поле (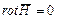
):
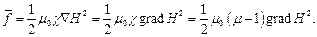
то есть на намагниченное тело действует сила пропорциональная градиенту квадрата напряжённости; ферромагнитный материал втягивается в область магнитного поля.
