План лекции. 1. Сколько неизвестных содержат первые два уравнения Максвелла?

Лекция №12

Контрольные вопросы

1. Сколько неизвестных содержат первые два уравнения Максвелла?

2. Что такое ток смещения и от чего он зависит?

3. Запишите скалярное произведение двух векторов в комплексной форме.

4. Сформулируйте и запишите в аналитической форме теорему Умова-Пойнтинга.

Теорема Умова-Пойнтинга в комплексной форме.

Примеры расчёта потоков мощности

1. Теорема Умова-Пойнтинга в комплексной форме.

2. Двухпроводная линия передачи, движение энергии в линии.

3. Передача энергии постоянного тока кабелем.

Краткое содержание лекции

В случае гармонического поля в линейной среде запишем систему уравнений Максвелла в комплексной форме:

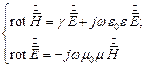
Первое уравнение заменяется сопряжённым и умножается на 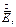второе умножается на :

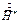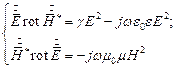
Вычтем из первого второе уравнение:

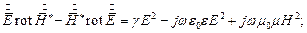
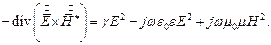(1)

Проинтегрируем (1) по некоторому объёму V:

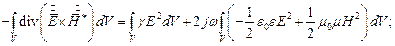
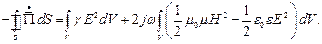
Полная мощность будет равна:

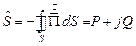
Активная и реактивная мощности равны:

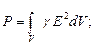
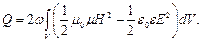
Двухпроводная линия

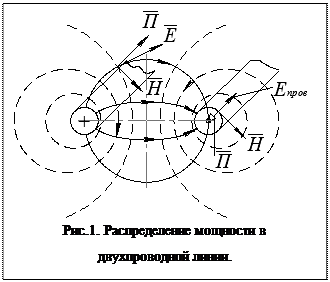В обыкновенной двухпроводной линии, с точки зрения изложенной теории вектора Пойнтинга, энергия передаётся через изолированную среду, окружающую провода, где векторы электрического и магнитного поля взаимно ортогональны, а вектор Пойнтинга параллелен проводам и направлен в сторону передачи энергии. При этом провода играют лишь роль направляющих. На рис.1 силовые и эквипотенциальные линии поля. Пунктиром показаны линии магнитного поля.

В каждой точке векторы напряжённости поля направлены по касательным к соответствующим линиям.

Внутри провода существует только продольная составляющая напряжённости электрического поля (заряды движутся вдоль провода), которая равна:

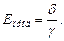
Эта составляющая есть и на поверхности провода. Она очень мала по сравнению с нормальной составляющей .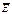

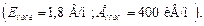
Однако существование продольной составляющей электрического поля определяет наличие составляющей вектора Пойнтинга, направленной по радиусу провода. Поток мощности, идущей в провод, представляет собой Джоулевы потери.

Передача мощности постоянного тока в кабеле.

Для определения мощности, передаваемой кабелем, воспользуемся выражением:

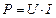
В диэлектрике, расположенном между внутренней жилой и оболочкой, передаётся мощность:

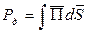
Найдём величину этой мощности:

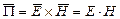
(поскольку 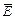и 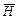– ортогональны) (рис. 2).

По закону полного тока:

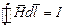или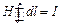

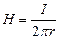
Для определения вектора напряжённости электрического поля запишем уравнение Лапласа для потенциала:

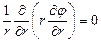
при граничных условиях: е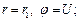сли если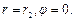

Интегрируя уравнение, находим:

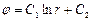
Используем граничные условия:

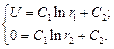
Вычитая из верхнего уравнения нижнее, получаем:

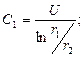
Таким образом, вектор Пойнтинга будет равен:

,

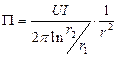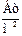
Мощность, передаваемая по диэлектрику, будет равной:

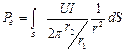
Элементарная площадка будет равна (рис.3):

.

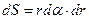
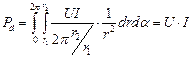Итак, вся мощность постоянного тока, передаваемая кабелем, передаётся не по металлу, а по диэлектрику изоляции.