Лекция №9
Контрольные вопросы
1. Какими величинами характеризуется магнитное поле?
2. Как с помощью закона полного тока можно рассчитывать магнитное поле?
3. В каких случаях магнитное поле можно считать потенциальным?
4. Каковы граничные условия для магнитного поля?
Векторный потенциал магнитного поля.
1. Вихревое поле, понятие векторного потенциала.
2. Закон полного тока в дифференциальной форме.
3. Уравнение Лапласа и Пуассона для векторного потенциала.
4. Граничные условия.
5. Расчёт поля с помощью векторного потенциала.
Краткое содержание лекции
В общем случае магнитное поле не является потенциальным. В случае, когда в поле не существует истоков вектор, определяющий интенсивность поля 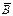 может быть представлен как вихрь некоторого другого вектора
может быть представлен как вихрь некоторого другого вектора 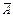 :
:
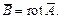 | (1) |
Это осуществимо, если 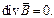
Этот вектор 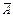 (Вб/м) называют векторным потенциалом поля
(Вб/м) называют векторным потенциалом поля 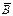 по аналогии со скалярным потенциалом, градиент которого определяет рассматриваемое поле.
по аналогии со скалярным потенциалом, градиент которого определяет рассматриваемое поле.
Необходимость условия равенства 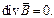 определяется тем, что по правилам операций векторного анализа дивергенция любого ротора тождественно равна нулю.
определяется тем, что по правилам операций векторного анализа дивергенция любого ротора тождественно равна нулю.
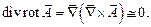 | (2) |
Так вектор 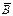 не имеет истоков, то он может быть представлен в виде (1). Магнитный векторный потенциал
не имеет истоков, то он может быть представлен в виде (1). Магнитный векторный потенциал 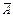 – это такая векторная функция, ротор которой равен вектору
– это такая векторная функция, ротор которой равен вектору 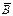 .
.
Из определения следует, что к вектору 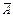 может быть прибавлена любая функция
может быть прибавлена любая функция 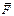 , ротор которой равен нулю, так как при этом
, ротор которой равен нулю, так как при этом
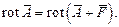
Функция 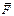 должна быть потенциальной.
должна быть потенциальной.
Закон полного тока можно представить в дифференциальной форме. Выполним преобразование:
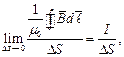
где ΔS – площадка, по контуру которой производится интегрирование.
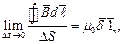
здесь 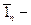 нормаль к площадке. По определению имеем
нормаль к площадке. По определению имеем
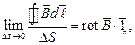
откуда получаем формулу для закона полного тока в дифференциальной форме:
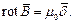 | (3) |
Подставляя (2) в (3), получаем соотношение
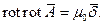
Согласно положениям векторного анализа:
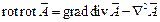 .
.
Обычно полагают, что при постоянном или медленно изменяющемся поле
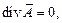
поэтому окончательно получаем уравнение Пуассона:
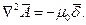 | (4) |
Решением этого уравнения является функция
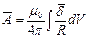 ,
,
или для проводника с током,

где 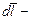 вектор, совпадающий с проводником тока; I – ток в проводнике.
вектор, совпадающий с проводником тока; I – ток в проводнике.
Для проекций уравнение (4) запишется как три уравнения:
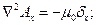

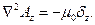
Если в рассматриваемой области вектор плотности тока равен нулю, то получается уравнение Пуассона:
 | (5) |
или
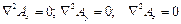
В декартовой системе координат уравнение (5) записывается в следующем виде:
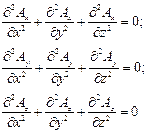 | (6) |
Граничными условиями уравнений (4) и (5) будет:

Решения уравнений (4) и (5) имеют аналитическое решение только в некоторых редких случаях, когда уравнение в частных производных можно свести к обыкновенному дифференциальному уравнению.
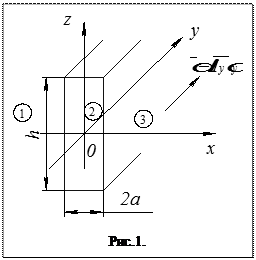 Пример
Пример
Найти вектор индукции в областях 1,2,3 для шины с током плотностью δу.
Для шины 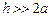 , поэтому
, поэтому 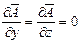 , и можно записать, что
, и можно записать, что 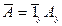 .
.
Для области 1 имеем 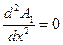 .
.
Для области 2 имеем 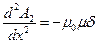 .
.
Для области 3 имеем 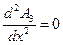 .
.
После интегрирования для трёх областей получаем следующие математические зависимости:
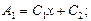
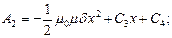
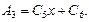
Определяем функции индукций для трёх областей:
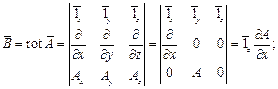
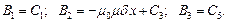
Имеются шесть неизвестных постоянных, для их определения используем граничные условия:
при 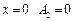 ; при
; при 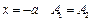 ; при
; при 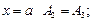
при 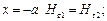 при
при 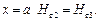
По закону полного тока: 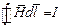
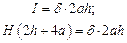
на границах: при 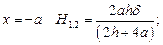
при 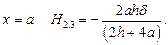
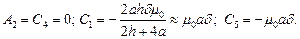
Получается система уравнений:
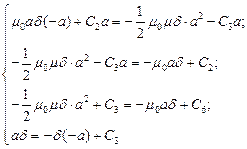
Тогда 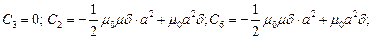


 2014-02-02
2014-02-02 1005
1005








