Лекция №7
Контрольные вопросы
1. На чём основан метод зеркальных изображений?
2. Что общего между методом зеркальных изображений и методом интегральных уравнений?
3. От чего зависит погрешность решения уравнения Лапласа численным методом?
4. Каким образом интегральные уравнения Фредгольма решаются численным методом?
Электрическое поле постоянного тока.
1. Вектор плотности тока.
2. Закон Ома в дифференциальной форме.
3. Закон Джоуля - Ленца в дифференциальной форме.
4. Аналогия электростатического поля и поля постоянного тока.
Краткое содержание лекции
 В массивных проводниках плотность и направление движения электрических зарядов не постоянна по всему объёму проводника. Плотность и направление движения электрических зарядов характеризуется вектором плотности тока
В массивных проводниках плотность и направление движения электрических зарядов не постоянна по всему объёму проводника. Плотность и направление движения электрических зарядов характеризуется вектором плотности тока 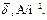 (рис.1).
(рис.1).
 Если в проводящем пространстве выделить малый цилиндр (рис.2) с размерами Δ l, ΔS, на длине цилиндра падает напряжение Uab и через него протекает ток I.
Если в проводящем пространстве выделить малый цилиндр (рис.2) с размерами Δ l, ΔS, на длине цилиндра падает напряжение Uab и через него протекает ток I.
Величина тока через поверхность ΔS равна:
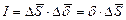
| (1) |
Падение напряжения на участке Δ l равно:
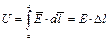
| (2) |
Активное сопротивление цилиндра:
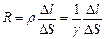
| (3) |
здесь ρ – удельное сопротивление, Ом·м,
γ – удельная проводимость материала, См/м.
Закон Ома в интегральной форме:
| U = I · R | (4) |
Перепишем (4) с учетом (1), (2), (3):
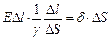
| (5) |
В итоге, получаем:
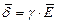 или или 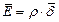
| (6) |
что и является законом Ома в дифференциальной форме.
Если найти сумму n площадок, то получится:
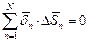 или
или 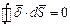 .
.
Это есть первый закон Кирхгофа в дифференциальной форме.
Если взять предел 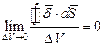 , то получится:
, то получится:
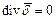 или или 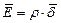
| (7) |
То есть линии вектора плотности тока непрерывны: какой ток входит в область ΔV, такой и выходит. Силовые линии нигде не начинаются и нигде не заканчиваются. Отсюда следует:
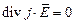 или
или 
Поле вектора 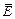 не имеет источников и является потенциальным:
не имеет источников и является потенциальным:
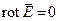
| (8) |
Закон Джоуля – Ленца в интегральной форме имеет вид:
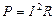
Найдём выражение для закона Джоуля – Ленца в дифференциальной форме:
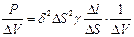 ,
,
здесь ΔV – объём цилиндра, 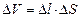 .
.
Даже имеем
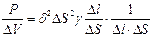
Итак, закон Джоуля – Ленца в дифференциальной форме (в точке) имеет вид:
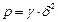
| (9) |
здесь р – удельная мощность, 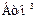 .
.
Проводимость γ как физическая величина не имеет себе равных по диапазону изменения, этот диапазон составляет девятнадцать порядков.
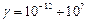
Порядок проводимостей для некоторых материалов следующий:
диэлектрик 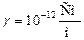 ; цветные металлы
; цветные металлы 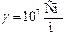 ;
;
земля 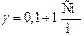 ; вода, спирт
; вода, спирт 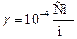 ;
;
раствор соли 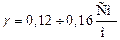 .
.
При переходе из одной проводящей среды в другую линии тока, если они не перпендикулярны плоскости перехода, меняют свое направление.
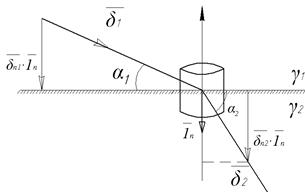
Рис 3. К выводу граничного условия
Из условия неразрывности линий тока ( ) следует, что ток, выходящий из первой среды, должен быть равен току, входящему во вторую среду:
) следует, что ток, выходящий из первой среды, должен быть равен току, входящему во вторую среду:
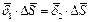
или
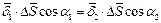 ,
,
откуда следует
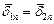
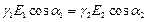
| (10) |
Из условия потенциальности поля:
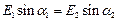
| (11) |
Разделив (11) на (10), получаем:
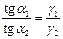
| (12) |
Если 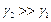 , то
, то 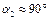 .
.
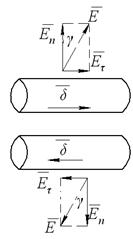 Граничные условия на поверхности двух проводников при прохождении тока не соответствуют условиям, которые имеют место в электростатике.
Граничные условия на поверхности двух проводников при прохождении тока не соответствуют условиям, которые имеют место в электростатике.
Поверхность проводника не эквипотенциальна. Кроме нормальной составляющей напряже-нности поля Еn, есть еще и тангенциальная составляющая, которая «гонит» заряды по проводнику. Естественно, что  . Нормальная составляющая поля в диэлектрике, а тангенциальная (касательная) – в проводнике.
. Нормальная составляющая поля в диэлектрике, а тангенциальная (касательная) – в проводнике.
Поскольку 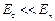 , на практике полагается, что имеется только нормальная составляющая поля на поверхности проводника.
, на практике полагается, что имеется только нормальная составляющая поля на поверхности проводника.
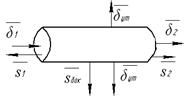 Рис. 4
Рис. 4
Для цилиндра Iут = I1 – I2, или
–I1 + I2 + Iут = 0.
Так как 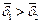 и
и 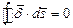 , то:
, то:
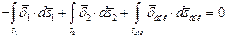
Рис. 5
Ток утечки
 Пусть к кабелю приложено напряжение U0 (рис.6). Тогда через изоляцию будет протекать ток утечки с плотностью
Пусть к кабелю приложено напряжение U0 (рис.6). Тогда через изоляцию будет протекать ток утечки с плотностью 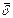 . Величина этого тока Iут.
. Величина этого тока Iут.
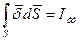 (13)
(13)
Поскольку 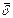 везде на некотором цилиндре радиуса r постоянен и совпадает по направлению с единичным вектором, нормальным к боковой поверхности цилиндра, то перепишется так:
везде на некотором цилиндре радиуса r постоянен и совпадает по направлению с единичным вектором, нормальным к боковой поверхности цилиндра, то перепишется так:
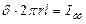 ,
,
здесь l – длина кабеля. Используя закон Ома 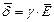 , получаем:
, получаем:
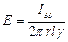
| (14) |
Для напряжения между жилой кабеля и оплеткой можно записать:
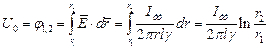
Откуда находим ток утечки:
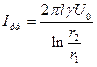
| (15) |
Сопротивление утечки будет равно:
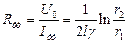
| (16) |
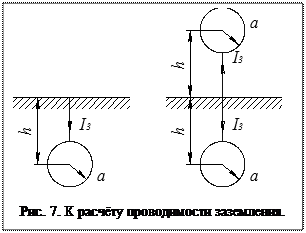
Проводимость заземления
Проводимость заземления для шара можно рассчитывать по формуле (рис. 7):
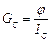 ,
,
где φ – потенциал металлического предмета; Iз – ток заземления.
Поскольку 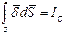 и
и 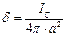 , то
, то 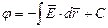 .
.
При 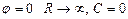 .
.
Тогда 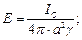
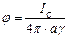 ;
; 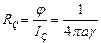 – сопротивление заземления для шара радиусом а.
– сопротивление заземления для шара радиусом а.
Для потенциала, создаваемого зеркальным изображением металлического шара на поверхности действительного шара при условии 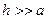 ,
,
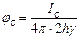
| (17) |
Суммарный потенциал будет равен:
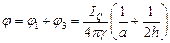
Откуда получаем:
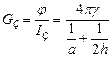 ; ; 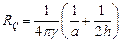
| (18) |
Чем больше металлическое тело и чем глубже оно зарыто в землю, тем сопротивление заземления меньше.
Аналогия между электростатическим полем и
полем постоянного тока
Электростатическое поле и поле постоянного тока являются потенциальными, то есть выполняется условие:
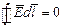 .
.
В таблице 1 приведены аналогичные величины.
Таблица 1. Аналогичные величины
| Электростатическое поле | Поле постоянного тока |
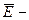 вектор напряжённости вектор напряжённости
| 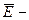 вектор напряжённости вектор напряжённости
|
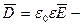 вектор индукции вектор индукции
| 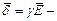 вектор плотности тока вектор плотности тока
|
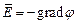
| 
|
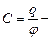 ёмкость ёмкость
| 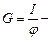 проводимость проводимость
|
| Граничные условия | |
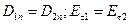
| 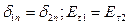
|
Вследствие существующей формальной аналогии между двумя полями, имеется метод анализа потенциальных полей, основанный на моделировании полей на электропроводной бумаге (рис. 8).
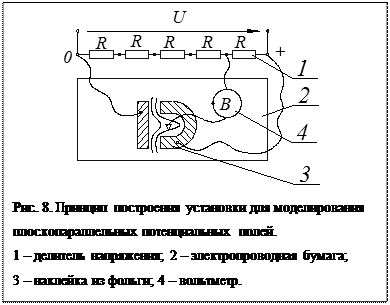
На электропроводной бумаге наклеивается токопроводящим клеем фольга, контур которой определяется моделируемой системой деталей. К фольге подводят напряжение. По электропроводной бумаге перемещается щуп, в цепи которого находится вольтметр, по которому определяется нулевой потенциал. С помощью щупа проводятся эквипотенциальные линии.
 2014-02-02
2014-02-02 506
506








