Лекция №8
Контрольные вопросы
1. Что такое законы в дифференциальной форме, чем эта форма отличается от интегральной?
2. Запишите формулы для законов Ома и Джоуля - Ленца в дифференциальной и интегральной формах.
3. В каком порядке рассчитывается сопротивление утечки и проводимость заземления?
4. Опишите метод моделирования потенциальных полей на электропроводной бумаге. На чём основан этот метод?
Магнитное поле. Основные величины, характеризующие магнитное поле.
1. Индукция магнитного поля, закон полного тока в интегральной форме.
2. Закон Био-Савара.
3. Напряжённость и намагниченность магнитного поля.
4. Потенциальное (квазистатическое) магнитное поле.
Краткое содержание лекции
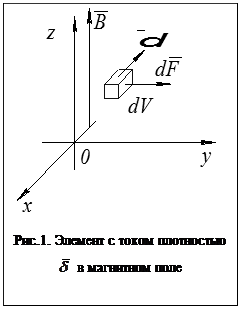 Интенсивность магнитного поля определяет векторная величина
Интенсивность магнитного поля определяет векторная величина 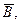 которая называется индукцией. То есть индукция является мерой магнитного поля.
которая называется индукцией. То есть индукция является мерой магнитного поля.
Если в некотором пространстве с током выделить объём dV, в котором плотность тока 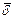 и этот объём находится в магнитном поле с индукцией
и этот объём находится в магнитном поле с индукцией 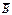 , то на него будет действовать сила, величина которой равна:
, то на него будет действовать сила, величина которой равна:
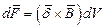
Если взять в проводнике с током I выделить малый отрезок 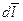 , то в магнитном поле с индукцией
, то в магнитном поле с индукцией 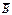 на него будет действовать сила равная
на него будет действовать сила равная
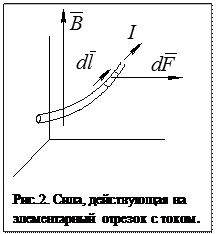
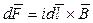
Магнитная индукция, обусловленная элементом тока, выражается формулой:
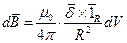 (1)
(1)
или для элемента проводника с током:
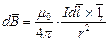
| (2) |
Принцип суперпозиции применим к магнитному полю, поэтому при заданном распределении вектора плотности тока в конечном объёме, индукция определяется формулой:
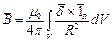 , Тл , Тл
| (3) |
или для проводника с током длиной 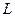
 , Тл , Тл
| (4) |
Иногда удобно говорить о поверхностном токе, вектор плотности которого 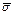 определяется так: пусть в тонком примыкающем к поверхности слое толщиной b распределён ток, имеющий плотность
определяется так: пусть в тонком примыкающем к поверхности слое толщиной b распределён ток, имеющий плотность 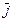 (вектор
(вектор 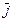 параллелен поверхности
параллелен поверхности 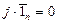 ). Если произведение
). Если произведение 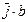 остаётся конечным при
остаётся конечным при 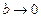 , то говорят о векторе поверхностного тока
, то говорят о векторе поверхностного тока 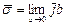 .
.
Магнитное поле, обусловленное поверхностным током:
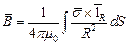
| (5) |
Везде в (3), (4), (5) векторы 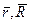 проводятся в точку наблюдения из точек расположения элементов с током.
проводятся в точку наблюдения из точек расположения элементов с током.
Формулы (3), (4) и (5) называются законом Био-Савара.
Для магнитного поля существует фундаментальный закон полного тока, который записывается так:
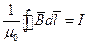
| (6) |
Интеграл по замкнутому контуру вектора индукции 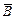 равен току, который охватывает этот контур. Если контур охватывает несколько проводников с током, то (6) запишется так:
равен току, который охватывает этот контур. Если контур охватывает несколько проводников с током, то (6) запишется так:
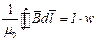
где w – количество витков с током.
Если имеется контур с током I и площадкой 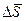 , то он обладает магнитным моментом равным:
, то он обладает магнитным моментом равным:
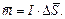
Намагниченность - магнитная поляризованность вещества, она определяется магнитным моментом единицы объёма
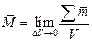 , А/м , А/м
| (7) |
Из самого определения намагниченности следует, что магнитный момент элементарного объёма dV намагниченного тела равен:
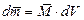
Если ферромагнитное тело намагничено, то можно представить, что магнитное поле создаётся поверхностным током 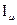 , линейная плотность которого
, линейная плотность которого 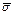 :
:
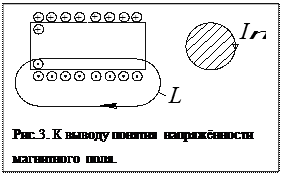
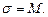
Тогда на основе закона полного тока можно записать для контура 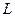 :
:
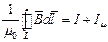
или 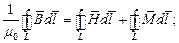
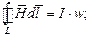
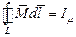
Откуда следует, что:
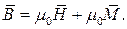
| (8) |
Вектор 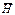 связан только с током в обмотке I и называется вектором напряжённости магнитного поля, измеряется в А/м.
связан только с током в обмотке I и называется вектором напряжённости магнитного поля, измеряется в А/м.
Преобразуем (8) таким образом:
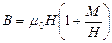
Обозначим 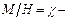 магнитная восприимчивость ферромагнитного вещества.
магнитная восприимчивость ферромагнитного вещества.
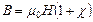
| (9) |
где величина 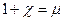 – относительная магнитная проницаемость ферромагнитного вещества.
– относительная магнитная проницаемость ферромагнитного вещества.
Окончательно получаем:
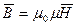
| (10) |
Рассмотрим особенности поля вектора 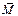 .
.
Возьмем достаточно малую площадку S, которую обтекает ток i (рис. 4). Положение вектора в пространстве определяется единичным вектором, нормальным к поверхности площадки  . Тогда вектор
. Тогда вектор 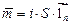 называется магнитным моментом. Единица измерения момента А·м2.
называется магнитным моментом. Единица измерения момента А·м2.
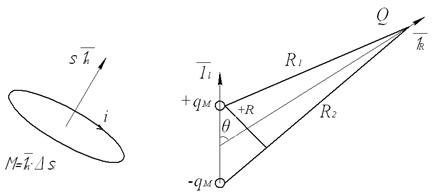
Рис. 4. Магнитный момент Рис. 5. Магнитный диполь
Ток i, обтекающий площадку S, создает такое же магнитное поле, как и диполь магнитных зарядов 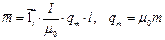 (рис. 5).
(рис. 5).
Магнитный потенциал, создаваемый в точке Q, будет равным:
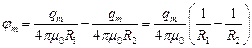
При условии, что 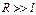 , можно записать:
, можно записать:
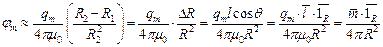
Напряженность магнитного поля диполя определяется так:
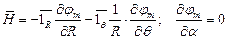
Запишем проекции вектора напряженности поля диполя:
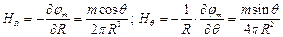
Если некоторый объем разобьем на элементарные области (рис. 6), в каждой из которых будет находиться диполь с моментом m, то в точке Q магнитный потенциал определяется следующим выражением:
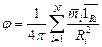 , ,
| (11) |
где N – количество элементов в объеме.
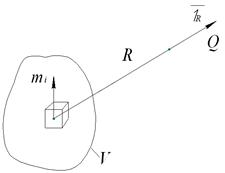
Рис. 6. Намагниченность объема
Поскольку намагниченность – это 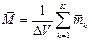 , можно записать:
, можно записать:
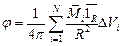 ,
,
а при 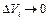 имеем
имеем 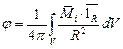
Определим вектор напряженности магнитного поля в точке Q, создаваемый намагниченным телом V:
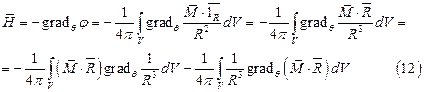
Так как приращение функции векторного аргумента равно
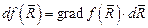 ,
,
то 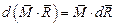 из-за того, что
из-за того, что 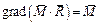 .
.
Поэтому выражение (13) сводится к следующему:
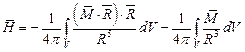
| (13) |
Обратите внимание, что от диполей напряженность поля убывает как 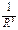 .
.
Если задана объемная плотность магнитных зарядов ρМ, то скалярный магнитный потенциал рассчитывается по формулам:
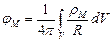 ,
,
или, так как 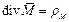 ,
,
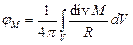
Напряженность магнитного поля при этом равна:
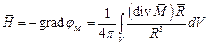
| (14) |
Если в объёме, где нет токов, проводимость магнитное поле можно считать потенциальным (квазистатическим) и для него справедливо:
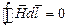 , ,
| (15) |
то можно ввести скалярный магнитный потенциал 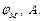 Тогда:
Тогда:
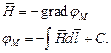
Расчёт такого поля можно производить теми же методами, что и расчёт электростатических полей, то есть методом решения уравнений Лапласа, Пуассона:
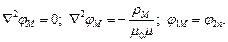
где ρМ – объёмная плотность магнитных зарядов.
Граничные условия при этом равны: 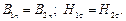
При расчёте магнитного поля можно использовать метод зеркальных изображений, независимо от того, является ли поле потенциальным или имеется область с током. При зеркальном изображении ток в проводнике и в зеркальном изображении проводника имеют одинаковое направление (рис. 7).

Рис. 7. Метод зеркальных изображений
При конечном значении μ2 задача по расчету магнитного поля (задача Сирла) решается следующим образом (рис. 8).
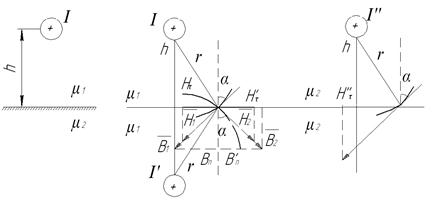
Рис. 8. Задача Сирла
Заменим поле в верхней полуплоскости полем двух токов I и I’, а поле в нижней – полем тока I’’. На границах двух сред имеем:
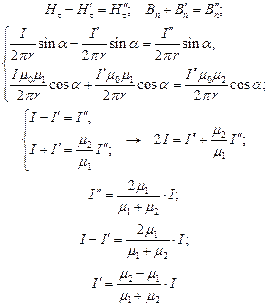
 2014-02-02
2014-02-02 688
688








