Количественную оценку уровня риска можно осуществлять с разной степенью точности расчетов. Рассмотрим наиболее упрощенный метод оценки рисков.
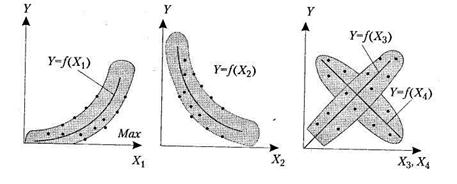
На первом этапе рекомендуется попытаться установить зависимости между внешними (внутренними) факторами и уровнем риска. Количество зависимостей определяется полнотой и качеством информационного обеспечения системы управления рисками. Для этих целей следует строить корреляционные поля (рис. 3, б, в) и устанавливать статистические зависимости.
а) б) в)
Рис. 3. Корреляционные поля зависимостей уровня риска (У) от факторов риска (Х1, Х2, Х3, Х4)
На рис. 3 показаны криволинейная (Xt) и прямолинейная (Х3) прямо пропорциональные зависимости факторов от функции (риска) и соответствующие обратно пропорциональные зависимости (Х2 и Х4).
В первом случае (X1 и Х3) с увеличением (ростом, повышением) фактора растет риск вложения инвестиций или выполнения какого-либо проекта. Например, с повышением степени износа основных производственных фондов (постоянного капитала) организации, среднего возраста технологии, текучести кадров, среднего возраста работников (преподавателей, ученых, специалистов) и других аналогичных факторов растет риск вложения инвестиций.
Во втором случае с уменьшением (снижением) фактора риск инвестиций растет (Х2 и Х4). Например, с падением конкурентоспособности (объектов (специалистов, менеджеров, технологии, оборудования, продукции, организации и т. д.), научного уровня принимаемых управленческих решений, средней заработной платы работников, фондовооруженности труда, социальной обеспеченности работников и других факторов аналогичного характера действия риск инвестиций растет.
Для использования этого инструмента управления рисками необходимо:
1) сделать отбор внешних и внутренних факторов риска, охватывающих макросреду, инфраструктуру региона и микросреду организации;
2) наладить мониторинг за этими факторами;
3) проранжировать факторы с целью отбора важнейших из них (управлять или осуществлять мониторинг за всеми факторами невозможно);
4) установить форму связи между факторами и уровнем риска;
5) попытаться установить количественные зависимости (уравнения регрессии) между важнейшими факторами риска и уровнем риска;
6) определить эластичность между важнейшими факторами риска и уровнем риска вложения инвестиций.
Кроме выполнения этих исследований необходимо установить количественные зависимости между конечными показателями проекта (прибылью, доходностью, ликвидностью и др.) и уровнем риска. Например, зависимость между уровнем риска и прибылью (доходностью) от вложения инвестиций описывается кривой Y = f(X3), риском и ликвидностью ценных бумаг кривой Y = f(X2), риском и устойчивостью функционирования организации функцией Y = f(X4), и т. д.
При оценке рисков следует рассчитывать вероятность достижения запланированного значения прибыли, которая описывается законом Гаусса (рис. 4).
Для того чтобы управленческие решения в инновационных проектах находились в зоне + на рис. 4, необходимо исследовать влияние внешних и внутренних факторов риска на прибыль, снизить влияние негативных (повышающих риск) факторов на прибыль и оптимизировать уровень риска.
Поэтапная оптимизация риска представляет собой:
1) отбор и ранжирование факторов внешней и внутренней среды объекта и субъекта риска с применением методов факторного анализа (математико-статистические и экспертные);

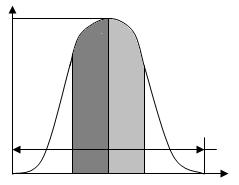
 -зона реальной прибыли
-зона реальной прибыли

-зона допустимых убытков
-зона критических убытков и прибыли (внутри кривой)
2) установление зависимостей между отобранными факторами риска и объектом риска (доходом, прибылью и др.);
3) стохастическую оптимизацию риска.
Вероятность (частоту) получения прибыли или потерь можно определить по формуле:
(1)
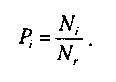
где Рi - вероятность получения прибыли или убытков в i-м случае;
Ni – число i- х случаев получения прибыли или убытков;
Nr - общее число случаев в генеральной выборке.
Среднее ожидаемое значение прибыли (потерь) определяется по формуле
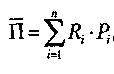
где i =1,2...n - номер случая(события); Ri-фактическое значение i-гo случая.
Среднеквадратическое отклонение (S) фактических данных по риску от расчетных определяется по формуле:
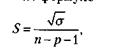
где s - дисперсия; п - число случаев наблюдения; р - число параметров уравнения (в данном примере — один).
Чем больше «S», тем выше риск прогнозируемого события, больше разброс, поле допуска (см. рис. 4) анализируемого параметра от средней величины (медианы, точка «0» на рис. 4), тем «грубее» модель
оптимизации риска. Необходимо сглаживать, избегать, уменьшать факторы риска с тем, чтобы сузить поле «S», поле риска. Хорошо, когда «S» меньше ±15%.
 2014-02-02
2014-02-02 1649
1649








