Фазовые методы исследования нелинейных систем

Нелинейные системы

На практике линейные системы встречаются достаточно редко, так как статические характеристики реальных объектов как правило не линейны. Если литаризация этих характеристик не обеспечивает требуемую точность оценки свойств объекта, то систему приходится рассматривать как не линейную.

Причины нелинейности:

· зазоры в кинематических цепях

· сухое трение

· явление гистерезиса

Основные особенности не линейных систем:

· неприменимость принципа суперпозиции, зависимость от последовательности приложения внешних воздействий

· в не линейных системах – понятие устойчивости. В этих системах говорят об устойчивости отдельных движений в системе

· могут возникать автоколебания, т.е. колебания поступательной частоты и амплитуды, которые поддерживаются за счет внутренней энергии системы

Различают: однозначные и неоднозначные характеристики.

· Однозначная нелинейность: характеризует связи выходного и входного сигнала описывается одной и той же зависимостью, как при увеличении, так и при уменьшении входного сигнала.

· Неоднозначная зависимость

Типовые однозначные нелинейности:

1. нечувствительность – изменение сигнала на входе, не влечет за собой изменение сигнала на выходе

2. насыщение

3. релейность

4. нечувствительность с насыщением

5. нечувствительность с релейностью

Типовые неоднозначные:

1. гистерезис с насыщением

2. гистерезис с релейностью

3. гистерезис с насыщением и нечувствительностью

Нелинейность существенно влияет на характер гармонического сигнала, перестает быть гармоничным, хотя он остается периодическим

Вид нелинейности определяет вид сигнала, начинающегося на выходе системы, если на ее вход подается гармоничный сигнал.

Наличие нелинейных элементов в системе приводит к необходимости описания поведения таких систем, с помощью дифференциальных уравнений высоких порядков. Очень часто решений таких уравнений в конечном виде не существует, поэтому для описания поведения нелинейных систем широко используют приближенные графоаналитические методы, один из которых является фазовый метод.

Сущность фазового метода: состояние нелинейной системы, в любой момент времени представленная в виде некоторой изображающей точки М фазового пространства, координатами которых является выходная величина системы и ее производные по времени:

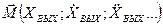
Изменение состояния системы приводит к изменению координат изображающей точки, таким образом при применении состояния системы изображающая точка перемещается в фазовом пр-ве по некоторой траектории – фазовая траектория.

Для исследования систем, используется фазовая плоскость:

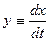
Время в явном виде не отражается на фазовой траектории.

Совокупность фазовых траекторий, характеризующих возможные движения в системе, называется фазовым портретом системы.

Для получения уравнения фазовой траектории используется дифференциальное уравнение системы:

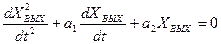(16.1)

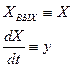
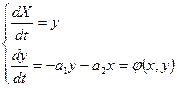
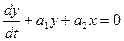
Делим первое выражение на второе:

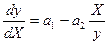– выражение для определения фазовых траекторий (16.2)

Свойства фазового портрета:

· если функция непрерывна и дифференцируема, то через любую точку фазовой плоскости можно провести одну единственную фазовую траекторию. Исключение: особые точки, для которых выполняется условие:

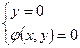– точки равновесия и именно в этих точках фазовые траектории могут пересекаться.

· В верхней фазовой полуплоскости, движение по фазовым траекториям происходит слева на право и наоборот (в нижней):

· Фазовые траектории пересекают ось Х под прямым углом, за исключением …… особых точек

· Особые точки, расположенные на оси абсцисс соответствуют состояниям равновесия и остановке движения