Дифференцирование одного переменного
Опр. f: (a,b)→𝑅 ф действительного переменного
Взяв произвольную т.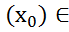 (а,в) составим отн:
(а,в) составим отн:
 где а<x<b,x≠
где а<x<b,x≠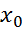
УтвА.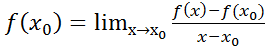 наз производным
наз производным 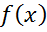 в т.
в т.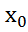
УтвБ. 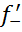 (
(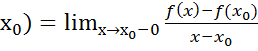 наз левосторонней произв
наз левосторонней произв
УтвГ.если один из пределов А,Б,В=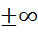 ,то соотв производная наз бесконечной произв.
,то соотв производная наз бесконечной произв.
УтвД.если f: [a,b]→𝑅 то в конечных т. [a,b]необх и достаточно чтобы сущ-али равные односторонние произв в т.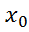
(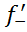 (
(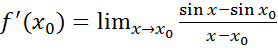 =
=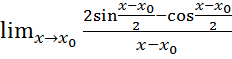 =
= 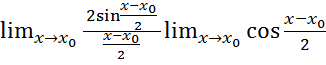 =
=
Пр2.f(x)=│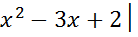 x=1 x=2
x=1 x=2
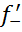 (
(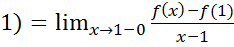 =
=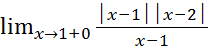 -
-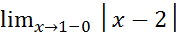
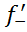 (
(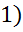 aпроизв не сущ-ет
aпроизв не сущ-ет 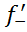 (
( aпроизв не сущ-ет
aпроизв не сущ-ет
Пр3.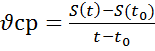 если
если 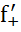 (
( =
=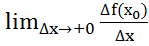 ,
,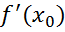 ,тогда:tg
,тогда:tg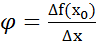 , ∆x→0,то секущая становится касательной,то tg
, ∆x→0,то секущая становится касательной,то tg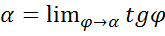 =
=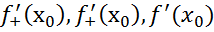 бесконечные произв, то соотв касательные ║ оси ОУ
бесконечные произв, то соотв касательные ║ оси ОУ
У=f( =K(x-
=K(x-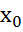 )ур-е прямой,проходящей через т.
)ур-е прямой,проходящей через т.
К=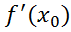 (x-
(x-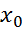 )ур-е касательной,проходящей через т
)ур-е касательной,проходящей через т
Опр3.Прямая линия ┴к касательной в т(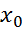 ,f(
,f(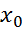 )) и проходящая через т. наз нормалью кривой у= f(
)) и проходящая через т. наз нормалью кривой у= f(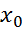 ) в т(
) в т(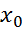 ,f(
,f(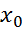 ))
))
 ,тогда если
,тогда если 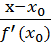
 2014-02-02
2014-02-02 413
413








