Опр1. f: (a,b)→𝑅 наз дифференцированной в т.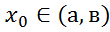 если её приращение в этой т. можно представить в виде (А=const
если её приращение в этой т. можно представить в виде (А=const 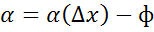 действ переменного от ∆х) ∆f(
действ переменного от ∆х) ∆f(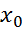 )=А∆х+
)=А∆х+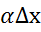
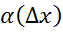 →0,∆х→0
→0,∆х→0
f: (a,b)→𝑅 наз дифференцированной на (а,в) если она диф в каждой т этого мн-ва
Теор:Условия диф функций одного переменного
Для того,чтобы f: (a,b)→𝑅 наз диф в т.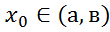 необх и достаточно чтоб она имела в этой т.конечную произв
необх и достаточно чтоб она имела в этой т.конечную произв
Док-во:1)Необходимость
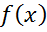 диф в т.
диф в т.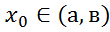 это значит: ∆f(
это значит: ∆f(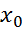 )=А∆х+
)=А∆х+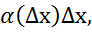 А=const,
А=const,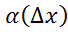 →0,∆х→0
→0,∆х→0
∆f(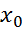 )=А+
)=А+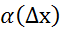 А=
А=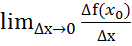 =
=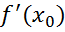 ,т.е
,т.е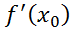 =
=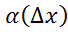 ,где
,где 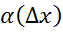 →0,∆х→0│*∆х(груп слаг)
→0,∆х→0│*∆х(груп слаг)
∆f(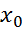 )=
)=
На осн т. о связе беск малых величин с пределами можно записать: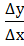 =
=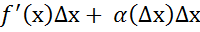 т.о приращение ф ∆у состоит из 2х слагаемых:линейного относительного ∆х,нелинейного
т.о приращение ф ∆у состоит из 2х слагаемых:линейного относительного ∆х,нелинейного
Опр.Дифференциалом ф-ции наз главная,линейная отн ∆х часть приращения ф-ции,равная произведению производной на приращение независимой переменной
Пр.Найти диф ф-ции у=х
dy=dx=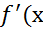 )dxa
)dxa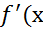 )∆x ∆y=KN
)∆x ∆y=KN



 Т.о дифференциал ф-ции есть приращение ординаты касательной,проведенной к гр ф в данной т,когда х получает приращение ∆х
Т.о дифференциал ф-ции есть приращение ординаты касательной,проведенной к гр ф в данной т,когда х получает приращение ∆х
|
|
|
С-ва дифференциала
dc=0; d(cu)=c du; d(u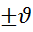 )=du
)=du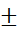 d
d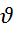 ; d(u
; d(u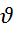 )=
)=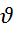 du+ud
du+ud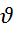 ; d(
; d(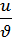 )=
)=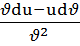 ;
;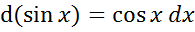 ;d(ctgx)=
;d(ctgx)=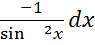
Инвариантность формы дифференциала
Пусть х=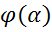 у=f(
у=f(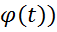
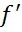 (
(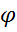 )
)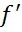 (x)
(x)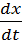 )dt
)dt
dy=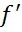 (x)
(x)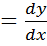 ;
; 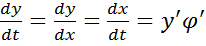
 2014-02-02
2014-02-02 290
290








