1)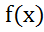 разрывна в т.
разрывна в т.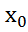 если она не явл. непрерывной в этой т.
если она не явл. непрерывной в этой т.
2)Если 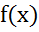 разрывна в т.
разрывна в т.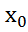 и если сущ-ет конечное знач-ие
и если сущ-ет конечное знач-ие 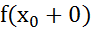 и
и 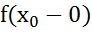 , то говорят, что
, то говорят, что 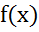 имеет в
имеет в 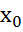 разрыв 1рода,в противном случае он наз разрывом 2 рода.
разрыв 1рода,в противном случае он наз разрывом 2 рода.
Разновидности разрыва 1 рода


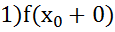 ≠
≠ 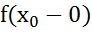 разрыв типа конечного скачка
разрыв типа конечного скачка
Скачёк ф=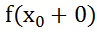 -
- 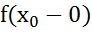
 2)
2) 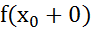 =
= 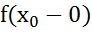 ≠
≠ 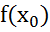 устранимый разрыв
устранимый разрыв
Устранение разрыва: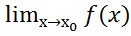 значение ф в т.
значение ф в т.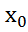 полагаем=lim
полагаем=lim
Разновидности разрывов 2рода
1)один из пределов бесконечный 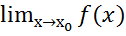 =
=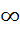 или
или 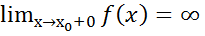 или
или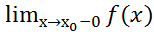 =
=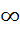 бесконечный разрыв
бесконечный разрыв
 2)Хотя бы один из односторонних пределов не сущ-ет
2)Хотя бы один из односторонних пределов не сущ-ет
у=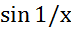 чем ближе к 0 тем чаще колебания
чем ближе к 0 тем чаще колебания
 в 0 значения не определено
в 0 значения не определено
Пр1 у=arctg1/x

 Ф непрерывна во всех т кроме 0
Ф непрерывна во всех т кроме 0
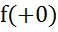 =
=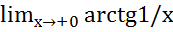 =
=
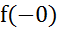 =
=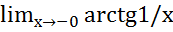 =
=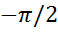
 =
=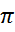 -скачёк ф
-скачёк ф
 | |||
 |
Пр2 ф-я «антье от х» у=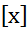
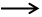 В т.х=К К
В т.х=К К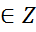

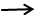
 f(K+0)=
f(K+0)=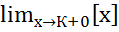 =К
=К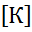 =f(K)
=f(K)
разрыв 1рода
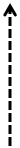
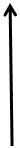 Пр3 у=1/х-1
Пр3 у=1/х-1
Ф непрерывна во всех т кроме 1
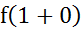 =
= 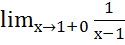 =+
=+ 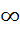

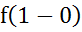 =
= 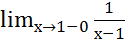 =-
=- 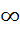
разрыв 2 рода
 2014-02-02
2014-02-02 633
633








