Опр1.Пусть задана f: (a,b)→𝑅
УтвА.Будем говорить,что 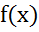 имеет локальный максимум в т.
имеет локальный максимум в т.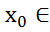 (а,в) если сущ-ет такая
(а,в) если сущ-ет такая 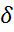 -окрестность т.
-окрестность т.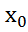 , что для всех х≠
, что для всех х≠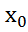 из этой окрестности,то вып f(
из этой окрестности,то вып f(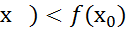
(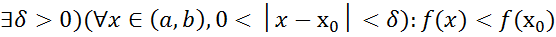
УтвБ. Будем говорить,что 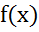 имеет локальный минимум в т.
имеет локальный минимум в т.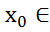 (а,в) если (
(а,в) если (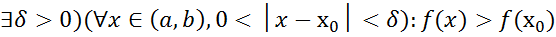 Локальные макс и мин объединяются под общим назв экстремум
Локальные макс и мин объединяются под общим назв экстремум
Опр2. Пусть задана f: (a,b)→𝑅 если в 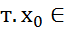 (а,в)выполн усл
(а,в)выполн усл 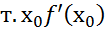
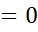 или не сущ-ет, то т
или не сущ-ет, то т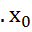 наз критической
наз критической
Теор:Необходимое усл экстремума.
Пусть задана f: (a,b)→𝑅 если t(x) имеет в т.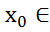 (а,в)локальный макс или лок минимум,то
(а,в)локальный макс или лок минимум,то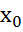 критическая т.
критическая т.
Док-во
1)Пусть в т.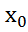 сущ-ет
сущ-ет 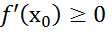 и
и 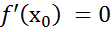

 2)Пр.
2)Пр.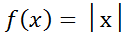 и
и 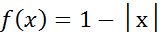
 1-лок макс;0-лок мин;0-крит т.
1-лок макс;0-лок мин;0-крит т.
Теор:1достаточное усл экстремума
Пусть f: (a,b)→𝑅удовл усл:
1.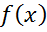 непрерывна на (а,в)
непрерывна на (а,в)
2.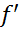 (х)>0 при х<
(х)>0 при х<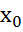 и
и 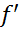 (х)<0 при х<
(х)<0 при х<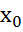 и
и 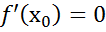 ,
,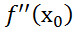 ≠0, тогда при
≠0, тогда при 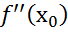 ≠0 в т
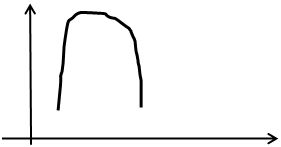
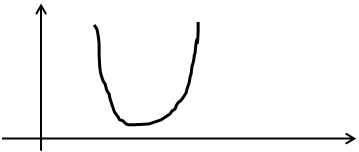
≠0 в т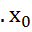 ф имеет макс, а при
ф имеет макс, а при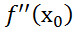 ≠0 в т
≠0 в т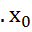 имеет min
имеет min
 |  | ||
 2014-02-02
2014-02-02 279
279








