Свойства интеграла по фигуре
Пусть, как предполагалось ранее, фигура  ─ ограничена и замкнута, а интегралы, о которых идет речь, существуют.
─ ограничена и замкнута, а интегралы, о которых идет речь, существуют.
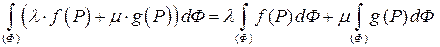 ,
,
где 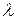 и
и  – константы.
– константы.
Это свойство следует из определения интеграла по фигуре и свойств пределов:
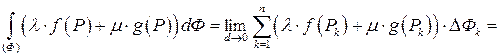
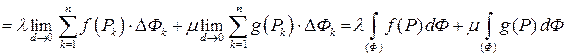 .
.
 2. Свойство аддитивности
2. Свойство аддитивности
Пусть фигура  разбита (рис. 6) на части
разбита (рис. 6) на части 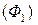 и
и 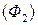 . Тогда
. Тогда
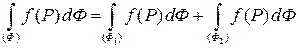 .
.
Так как интеграл по фигуре численно равен массе фигуры с плотностью  , то физический смысл этого свойства следующий: масса всей фигуры
, то физический смысл этого свойства следующий: масса всей фигуры  равна сумме масс ее частей
равна сумме масс ее частей 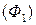 и
и 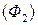 .
.
 2014-02-02
2014-02-02 1781
1781
