Теорема о среднем

Об оценке модуля интеграла

Об оценке интеграла

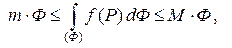
где 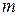и 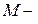наименьшее и наибольшее значения функции на фигуре .

Действительно, так как 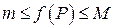на фигуре , то по свойствам 4, 1, 3

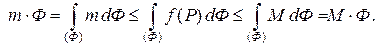
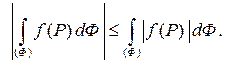
Оценка модуля интеграла следует из свойств модуля: .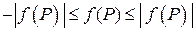

Тогда из свойства 5 следует

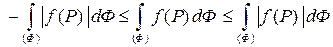и значит,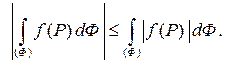

Пусть функция непрерывна на фигуре . Тогда на существует точка 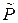такая, что

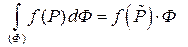или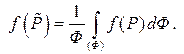

Выведем эту формулу. Так как функция непрерывна на фигуре , то она достигает на этой фигуре наименьшего 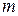и наибольшего 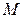значений. Поэтому 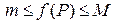на . Тогда из соотношения (6.4) следует:

.

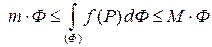Разделим это неравенство на положительное число :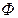

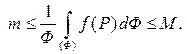
Рассмотрим число , равное 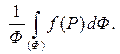Из равенства следует, что 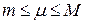. Так как функция непрерывна на фигуре , то она принимает на этой фигуре все промежуточные значения между 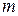и 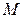. В частности, функция принимает промежуточное значение в некоторой точке 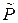фигуры , то есть 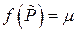. Отсюда 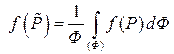и .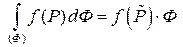

Замечание. Значение из теоремы о среднем называют средним значением функции на фигуре и обозначают 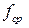. Оно используется в прикладных задачах.