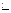1). Если фигура  является отрезком
является отрезком 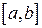 , то интеграл называют определенным интегралом и обозначают
, то интеграл называют определенным интегралом и обозначают 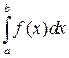 . По определению
. По определению
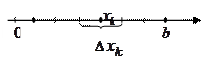
|
|
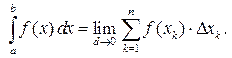
Здесь 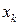 – координаты выбранных точек
– координаты выбранных точек 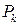 ,
, 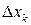 – меры ячеек разбиения, т.е. длины частичных отрезков,
– меры ячеек разбиения, т.е. длины частичных отрезков, 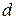 – максимальный из
– максимальный из 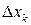 .
.
2). Если фигура  является дугой кривой
является дугой кривой 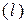 , то интеграл по такой фигуре называют криволинейным интегралом 1-го рода и обозначают
, то интеграл по такой фигуре называют криволинейным интегралом 1-го рода и обозначают

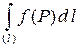 . По определению
. По определению
|
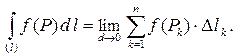
Здесь 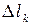 – меры ячеек, в данном случае длины частичных дуг
– меры ячеек, в данном случае длины частичных дуг 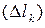 ;
; 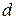 – максимальный из
– максимальный из 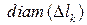 (рис. 2).
(рис. 2).
|
 является поверхностью
является поверхностью  , то интеграл по такой фигуре называют поверхностным интегралом 1-го рода и обозначают
, то интеграл по такой фигуре называют поверхностным интегралом 1-го рода и обозначают 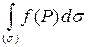 . По определению
. По определению
|
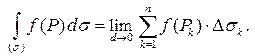
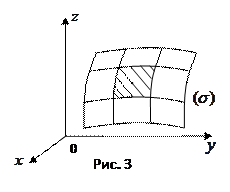
Здесь 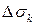 – меры ячеек, в данном случае их площади;
– меры ячеек, в данном случае их площади; 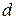 – максимальный из
– максимальный из 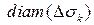 (рис. 3).
(рис. 3).
4). Если фигура  является плоской областью
является плоской областью 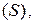 то интеграл по такой фигуре называют двойным интегралом и обозначают
то интеграл по такой фигуре называют двойным интегралом и обозначают 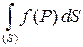 . По определению
. По определению 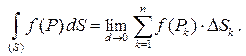
Здесь 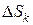 – меры ячеек, в данном случае их площади;
– меры ячеек, в данном случае их площади; 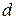 – максимальный из
– максимальный из 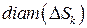 (рис. 4).
(рис. 4).
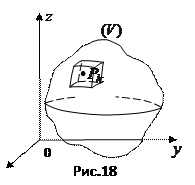
5). Если фигура  является телом
является телом 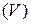 , то интеграл по такой фигуре называют тройным интегралом и обозначают
, то интеграл по такой фигуре называют тройным интегралом и обозначают 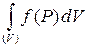 . По определению
. По определению
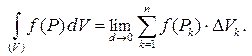
Здесь 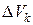 – меры ячеек, в данном случае их объемы;
– меры ячеек, в данном случае их объемы; 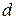 – максимальный из
– максимальный из 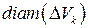 (рис. 5).
(рис. 5).
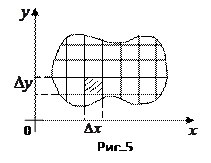
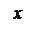 Рассмотрим еще одну часто употребляемую форму записи двойного интеграла. Двойной интеграл – это интеграл по плоской области
Рассмотрим еще одну часто употребляемую форму записи двойного интеграла. Двойной интеграл – это интеграл по плоской области 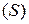 . Пусть эта область лежит в плоскости
. Пусть эта область лежит в плоскости 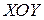 . Так как интеграл не зависит от способа разбиения фигуры на ячейки, то разобьем фигуру на ячейки прямыми, параллельными оси
. Так как интеграл не зависит от способа разбиения фигуры на ячейки, то разобьем фигуру на ячейки прямыми, параллельными оси  , с расстояниями
, с расстояниями 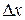 между ними и прямыми, параллельными оси
между ними и прямыми, параллельными оси 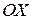 , с расстояниями
, с расстояниями 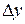 между ними (рис. 5). Тогда площадь любой ячейки, кроме приграничной, равна
между ними (рис. 5). Тогда площадь любой ячейки, кроме приграничной, равна 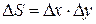 . Поэтому
. Поэтому 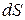 и интеграл записывают в следующем виде:
и интеграл записывают в следующем виде:
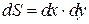 ,
,
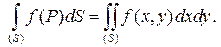
Аналогичная форма записи принята и для тройного интеграла
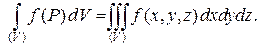
 2014-02-02
2014-02-02 1651
1651