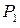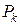Понятие интеграла по фигуре

Задача о вычислении массы фигуры

Рис. 1

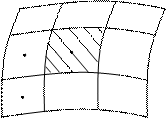
Пусть – произвольная фигура, в каждой точке 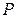которой известна плотность распределения массы 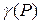. Разобьем фигуру на 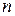малых ячеек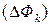 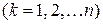. В каждой ячейке 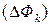выберем произвольную точку 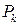(рис. 13). В силу малости ячейки ее плотность можно считать постоянной и равной 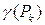. Тогда масса ячейки 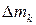приближенно равна произведению плотности на меру ячейки, т.е. 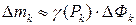. Суммируя массы всех ячеек, получим массу фигуры

.

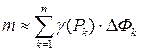Это приближенное равенство будет тем точней, чем меньше диаметры всех ячеек или максимальный из диаметров ячеек 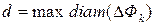. Точное значение массы фигуры определяется как предел суммы при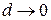

.

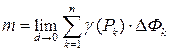Этот предел называют интегралом от функции 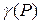по фигуре и обозначают 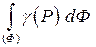. К пределам такого типа приводят и другие задачи. Абстрагируясь от конкретной задачи о массе фигуры, дадим общее понятие интеграла по фигуре.

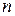Пусть на фигуре определена скалярная функция . Так же, как и в задаче о массе фигуры, разобьем фигуру на ячеек 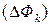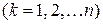. В каждой ячейке 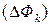выберем произвольную точку 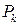. Составим сумму 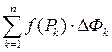. Эту сумму называют интегральной суммой функции по фигуре . Найдем предел интегральной суммы при стремлении к нулю 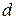(максимального из диаметров ячеек).

Если существует при 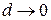предел интегральной суммы функции по фигуре , не зависящий от способа разбиения фигуры и выбора точек 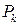, то этот предел называют интегралом функции по фигуре и обозначают 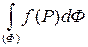. При этом функцию называют интегрируемой на фигуре .

Таким образом, по определению

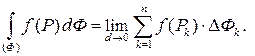
Естественно возникает вопрос: для каких функций существует интеграл по фигуре (то есть существует предел интегральных сумм, не зависящий от способа разбиения фигуры на ячейки и от выбора точек 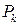). Ответ на этот вопрос дает следующая теорема, которую приводим без доказательства.

Теорема существования. Пусть функция непрерывна на фигуре 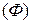. Тогда существует интеграл .

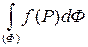Интеграл по фигуре может существовать не только для непрерывных функций, но и для кусочно-непрерывных функций. В дальнейшем будем предполагать, что интегралы, о которых идет речь, существуют.