Фигура и ее мера

Понятие интеграла по фигуре и его свойства

ЛЕКЦИОННОЕ ЗАНЯТИЕ. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ПРИЛОЖЕНИЯ. ИНТЕГРАЛЫ ПО ФИГУРЕ

Для единообразного введения интегралов нам понадобится понятие фигуры и ее меры.

Объединим общим названием “фигура” – отрезок 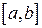, дугу 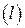, плоскую область 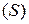, поверхность , тело 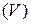. Отрезок и дугу назовем одномерной фигурой, плоскую область и поверхность – двумерной фигурой, тело – трехмерной фигурой.

С понятием фигуры связано понятие ее меры. Мерой одномерной фигуры назовем ее длину, мерой двумерной фигуры назовем ее площадь, мерой трехмерной фигуры назовем ее объем. Для фигур 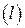, , 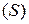, 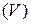их меры соответственно обозначим 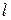, , 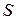, 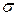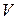. В общем случае фигуру обозначим , а ее меру – той же буквой 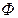, но без скобок.

Для дальнейшего изложения введем понятие диаметра фигуры. Назовем диаметром 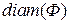фигуры наибольшее из расстояний между ее точками. Например, диаметр шара радиусом 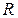равен 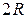, диаметр куба равен длине его диагонали.

В дальнейшем будем предполагать, что

1) фигура ─ ограничена, т.е. имеет конечный диаметр,

2) фигура ─ замкнута, т.е. включает границу.