Лекционное занятие. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Пусть фигура в плоскости 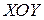 ограничена линиями
ограничена линиями 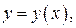
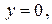
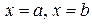 , причем
, причем 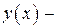 непрерывная неотрицательная функция на
непрерывная неотрицательная функция на 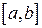 (рис. 1). Разобьем отрезок
(рис. 1). Разобьем отрезок 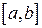 на
на 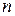 частичных отрезков с длинами
частичных отрезков с длинами 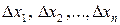 . Через точки деления проведем вертикальные прямые, которые разделят фигуру на
. Через точки деления проведем вертикальные прямые, которые разделят фигуру на 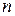
|
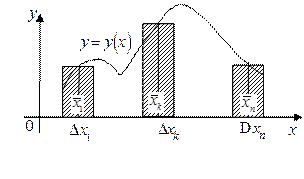
вертикальных полосок. Каждую 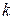 -ю вертикальную полоску заменим прямоугольником с основанием, равным
-ю вертикальную полоску заменим прямоугольником с основанием, равным 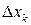 , и высотой, равной
, и высотой, равной 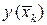 , где
, где 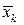 − произвольно выбранная точка на
− произвольно выбранная точка на 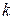 -м частичном отрезке. Площадь такого прямоугольника
-м частичном отрезке. Площадь такого прямоугольника
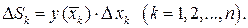
Суммируя площади всех прямоугольников, получим 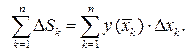
Площадь 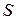 заданной фигуры определяется как предел полученной суммы
заданной фигуры определяется как предел полученной суммы 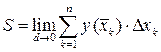 при стремлении к нулю
при стремлении к нулю  . Мы получили предел интегральной суммы непрерывной функции
. Мы получили предел интегральной суммы непрерывной функции 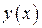 по отрезку
по отрезку 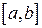 , то есть интеграл
, то есть интеграл 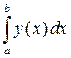 . Таким образом, площадь фигуры, ограниченной линиями
. Таким образом, площадь фигуры, ограниченной линиями 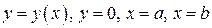 , при условии, что
, при условии, что 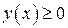 , вычисляется по формуле
, вычисляется по формуле
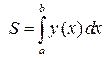 или
или 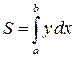 .
.
 Пример 1. Вычислить интеграл
Пример 1. Вычислить интеграл 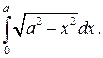
|
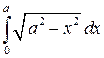 численно равен площади фигуры, ограниченной линиями
численно равен площади фигуры, ограниченной линиями 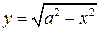 ,
, 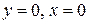 ,
, 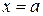 . Построим эти линии, учитывая, что уравнение
. Построим эти линии, учитывая, что уравнение 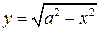 определяет ту часть окружности
определяет ту часть окружности 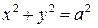 , где
, где 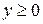 (рис. 2). Полученная фигура есть четверть круга с площадью
(рис. 2). Полученная фигура есть четверть круга с площадью 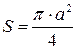 . Таким образом,
. Таким образом,|
|
|
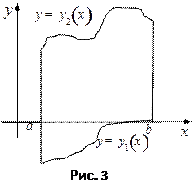
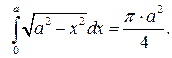
Перейдем к более общему случаю. Пусть фигура в плоскости 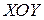 ограничена линиями
ограничена линиями 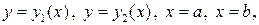 причем
причем 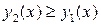 на
на 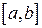 (рис. 3). Как и в предыдущем случае, можно получить следующую формулу для площади
(рис. 3). Как и в предыдущем случае, можно получить следующую формулу для площади 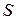 такой фигуры:
такой фигуры:
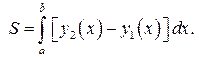
Иногда вычисления значительно упрощаются, если поменять ролями оси 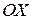 и
и  . Пусть фигура в плоскости
. Пусть фигура в плоскости 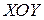 ограничена линиями
ограничена линиями 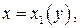
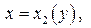
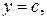
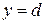 , причем
, причем 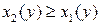 на отрезке
на отрезке 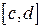 (рис. 4). Тогда
(рис. 4). Тогда
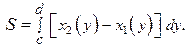
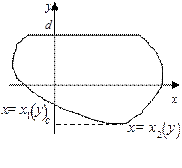 Пример 2. Вычислить площадь фигуры, ограниченной линиями
Пример 2. Вычислить площадь фигуры, ограниченной линиями 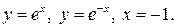
|
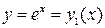 , сверху – линией
, сверху – линией 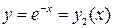 ,
, 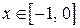 . Для вычисления площади фигуры воспользуемся формулой (7.11):
. Для вычисления площади фигуры воспользуемся формулой (7.11): 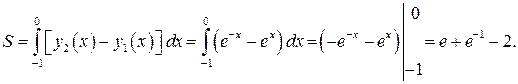

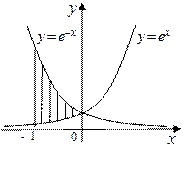 Пример 3. Вычислить площадь фигуры, ограниченной линиями
Пример 3. Вычислить площадь фигуры, ограниченной линиями 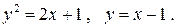
|
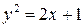 или
или 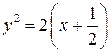 определяет параболу с вершиной
определяет параболу с вершиной 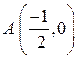 , осью симметрии − осью OX (рис. 6). Уравнение
, осью симметрии − осью OX (рис. 6). Уравнение 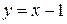 определяет прямую, проходящую через точки
определяет прямую, проходящую через точки 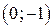 ,
, 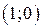 . Найдем точки пересечения параболы и прямой, решив систему уравнений:
. Найдем точки пересечения параболы и прямой, решив систему уравнений: 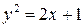 ,
, 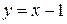 . Получим точку
. Получим точку 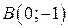 и точку
и точку 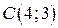 .
. 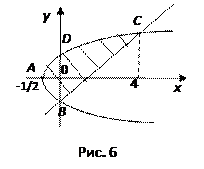 Вычислим площадь фигуры по формуле. Для этого нужно записать уравнения кривых, ограничивающих фигуру, в виде, разрешенном относительно
Вычислим площадь фигуры по формуле. Для этого нужно записать уравнения кривых, ограничивающих фигуру, в виде, разрешенном относительно  . Слева фигура ограничена дугой параболы CAB, на которой
. Слева фигура ограничена дугой параболы CAB, на которой 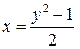 , справа – отрезком прямой BC, на котором
, справа – отрезком прямой BC, на котором 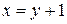 ; y меняется от
; y меняется от 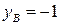 до
до 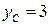 . Поэтому по формуле имеем
. Поэтому по формуле имеем
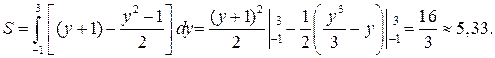
 2014-02-02
2014-02-02 1127
1127
