Воспользуемся формулой 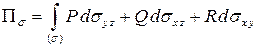 и рассмотрим интегралы
и рассмотрим интегралы
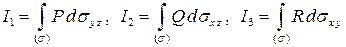 .
.
Для вычисления интеграла 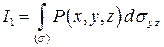 следует
следует
а) в подынтегральной функции заменить  его значением
его значением 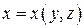 на поверхности,
на поверхности,
б) учесть, что 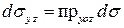 и поэтому
и поэтому 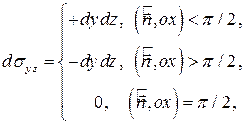
в) вычислить получающийся двойной интеграл по проекции 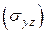 .
.
Для вычисления интеграла 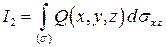 следует
следует
а) в подынтегральной функции заменить 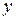 его значением
его значением 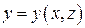 на поверхности,
на поверхности,
б) учесть, что  и поэтому
и поэтому 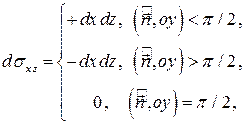
в) вычислить получающийся двойной интеграл по проекции 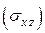 .
.
 Аналогично вычисляется интеграл
Аналогично вычисляется интеграл 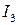 .
.
Пример 10.3. Вычислить поток поля 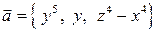 через поверхность цилиндра
через поверхность цилиндра 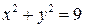
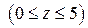 с выбранной внешней нормалью (рис. 5).
с выбранной внешней нормалью (рис. 5).
Решение. Для вычисления потока воспользуемся формулой
 .
.
1). Вычислим интеграл 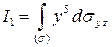 .
.
На части 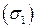 цилиндра, где
цилиндра, где 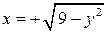 , имеем:
, имеем: 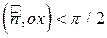 ,
, 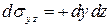 ;
;
на части 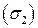 цилиндра, где
цилиндра, где 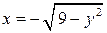 , имеем:
, имеем: 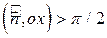 ,
, 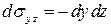 ;
;
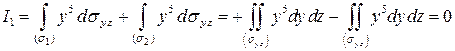 .
.
2). Вычислим интеграл 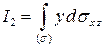 .
.
На части 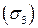 цилиндра, где
цилиндра, где 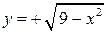 , имеем:
, имеем: 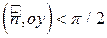 ,
, 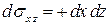 ;
;
на части 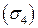 цилиндра, где
цилиндра, где 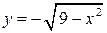 , имеем:
, имеем: 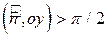 ,
, 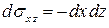 ;
;
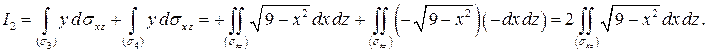 Проекция
Проекция 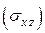 есть прямоугольник, поэтому
есть прямоугольник, поэтому
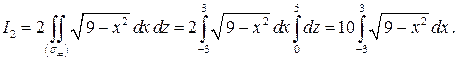
Воспользовавшись результатом примера 7.8, получим
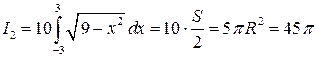 .
.
3). Вычислим интеграл 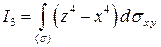 .
.
Так как на поверхности цилиндра 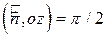 , то
, то 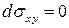 и поэтому
и поэтому 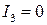 .
.
В результате 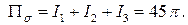
 2014-02-02
2014-02-02 1407
1407








