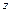2014-02-02
4568
Для вычисления потока воспользуемся формулой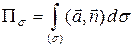 
и параметрическим уравнением поверхности 
: 
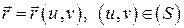. Вычислим нормальный вектор поверхности по формуле: 
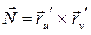; тогда единичный нормальный вектор 
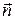, определяющий ориентацию поверхности, есть вектор
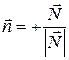, если 
, 
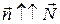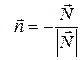, если 
.
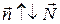Элемент площади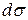 
вычислим по формуле (13.1): 
.
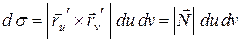Подставляя значения для 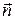и 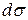в интеграл 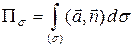, получим
.
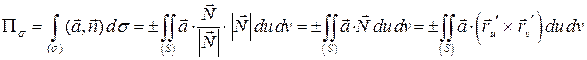Окончательно имеем:
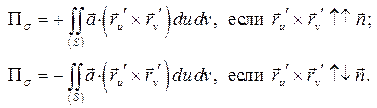
Пример 4. Вычислить поток поля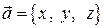 
через поверхность 
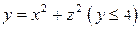, ориентированную внешней нормалью (рис. 6).
Решение. Запишем уравнение поверхности в параметрическом виде
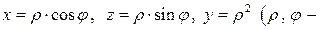параметры).
Найдем вектор
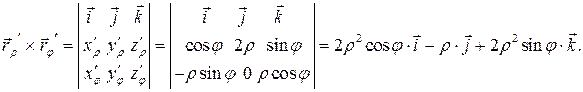
Вторая координата этого вектора отрицательна, как и у вектора 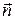, поэтому
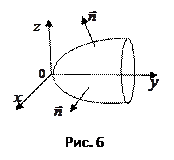
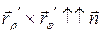и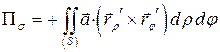 
;
.
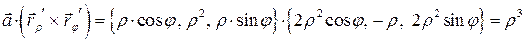Тогда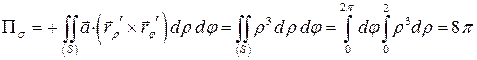 
.
Пример 5. Вычислить поток поля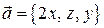 
через верхнюю сторону части плоскости 
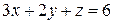, расположенной в первом октанте (рис. 3).
Решение. Вычислим поток методом проектирования на одну плоскость. Для этого запишем уравнение поверхности в параметрическом виде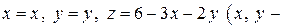 
параметры).
Найдем векторное произведение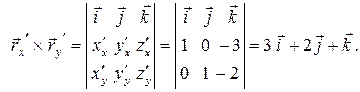 
Вторая координата этого вектора положительна, как и у вектора 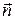, поэтому
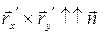и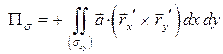 
.
Вычислим значение подынтегральной функции на поверхности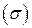 
:
.
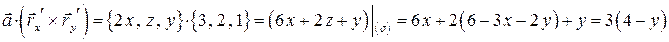Тогда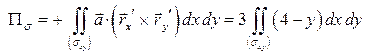 
. Этот интеграл был вычислен в примере 2: 
.
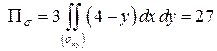14. Лекционное занятие. ФОРМУЛА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ
Поток векторного поля через замкнутую поверхность удобно вычислять по формуле Остроградского с помощью дивергенции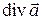 
поля 
:
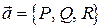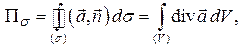где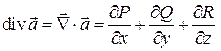 
.
В этой формуле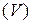 
─ тело, ограниченное замкнутой поверхностью ;
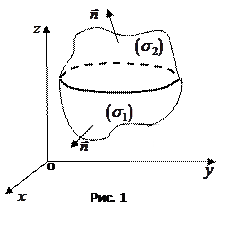поверхность ориентирована внешней нормалью; функции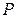 
, 
, 
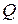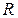непрерывны вместе со своими частными производными.
Вывод формулы проведем для случая, когда поверхность состоит (рис. 1) из поверхности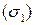 
с уравнением 
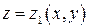и поверхности 
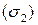с уравнением 
.
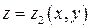Запишем формулу Остроградского в координатной форме
.
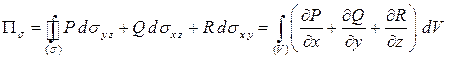Покажем сначала, что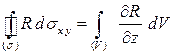 
. Действительно,
.
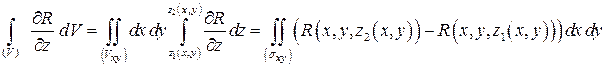С другой стороны,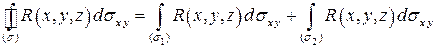 
.
На поверхности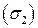 
: ; 
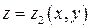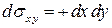, так как 
;
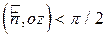на поверхности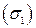 
: ; 
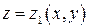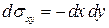, так как 
;
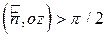поэтому
.
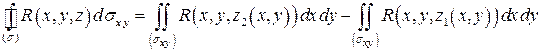Получившееся выражение равно правой части формулы, значит
.
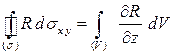Аналогично можно показать, что
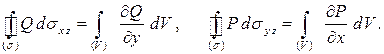
Складывая равенства, получим формулу Остроградского.
Пример 1. Вычислить поток поля 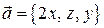через поверхность пирамиды, ограниченную плоскостью 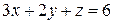и координатными плоскостями.
Решение. Так как поверхность замкнутая, то воспользуемся формулой Остроградского
.
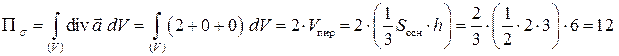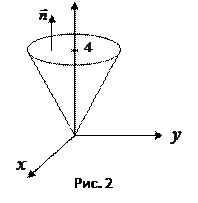Пример 2. Вычислить поток жидкости, текущей со скоростью 
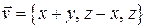, через боковую поверхность конуса 
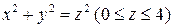в направлении внешней нормали (рис. 2).
|
|
.
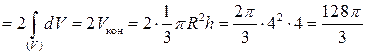Поток жидкости через основание конуса вычислим по формуле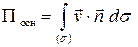 
.
Учтем, что единичный вектор нормали к основанию конуса равен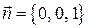 
. Поэтому 
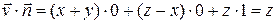. На основании конуса 
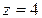, значит, 
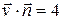и
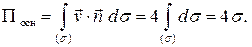
Здесь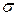 
─ площадь основания, т. е. площадь круга радиусом 4. Следовательно,
.
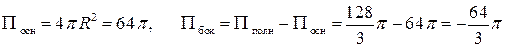Так как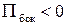 
, то через боковую поверхность конуса в направлении внешней нормали течет жидкости меньше, чем в противоположном направлении.
Остановимся более подробно на свойствах дивергенции.
