2014-02-02
1116
Потоком векторного поля 
через ориентированную поверхность 
с единичным нормальным вектором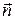 
называют величину
.
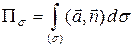Отметим, что при изменении ориентации поверхности вектор 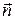заменяется на вектор 
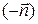и, следовательно, поток меняет знак.
Рассмотрим различные формы записи потока.
1). Обозначим через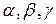 
углы между вектором 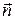и соответственно осями 
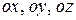. Тогда направляющие косинусы 
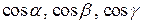являются координатами вектора 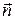, т.е. 
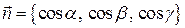. Если вектор поля имеет координаты 
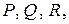то
.
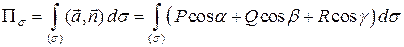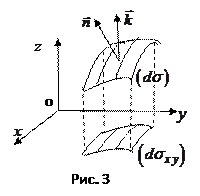2). Рассмотрим элемент площади 
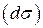и его проекцию 
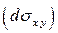на плоскость 
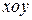(рис. 3). Угол между 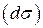и плоскостью 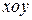равен углу между их нормальными векторам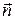и и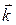 
, т.е. углу 
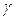. Поэтому
.
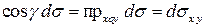Аналогично
, 
.
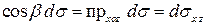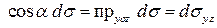Тогда
.
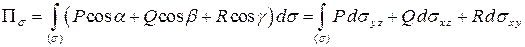3). Введем вектор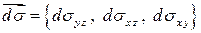 
, называемый векторным элементом площади. Так как 
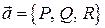, то из (10.4) следует
.
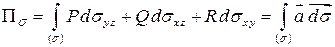Наиболее употребительны из получившихся следующие формы записи потока
.
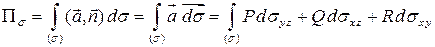Первые две формы записи потока в соотношении называют векторными, последнюю форму записи ─ координатной.
