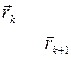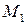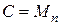Задача о работе силы
Линейный интеграл и циркуляция векторного поля
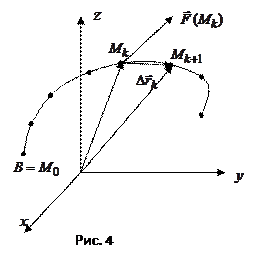
|
|
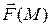 , под действием которых материальная точка движется по кривой
, под действием которых материальная точка движется по кривой 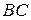 от точки
от точки 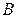 к точке
к точке 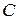 . Вычислим совершаемую при этом работу. Для этого разобьем линию
. Вычислим совершаемую при этом работу. Для этого разобьем линию 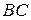 на
на 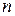 частей точками
частей точками 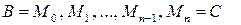 с радиус-векторами
с радиус-векторами 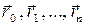 (рис. 66). Рассмотрим вектор перемещения
(рис. 66). Рассмотрим вектор перемещения
|
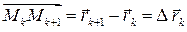
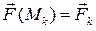 . Их скалярное произведение приближенно равно работе
. Их скалярное произведение приближенно равно работе 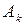 силы
силы 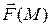 вдоль дуги
вдоль дуги 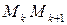 , т. е.
, т. е. 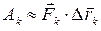 .
.
Вычислим работу вдоль всей линии 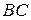 :
:
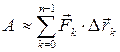 .
.
Это равенство будет тем точнее, чем меньше длины векторов 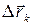 . Максимальную из этих длин обозначим
. Максимальную из этих длин обозначим 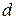 и, переходя к пределу при
и, переходя к пределу при 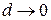 , определим точное значение работы
, определим точное значение работы
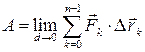 .
.
Этот предел обозначают 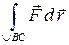 и называют линейным интегралом поля
и называют линейным интегралом поля 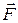 по дуге
по дуге 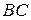 или криволинейным интегралом второго рода.
или криволинейным интегралом второго рода.
Отвлекаясь от физического содержания рассмотренной задачи, аналогичным образом вводят понятие линейного интеграла произвольного поля 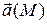 (риc. 4):
(риc. 4):
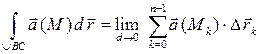 ,
,
где 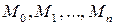 ─ точки разбиения дуги
─ точки разбиения дуги 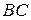 ,
, 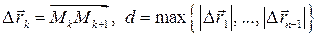 .
.
Отметим три свойства линейного интеграла:
1) 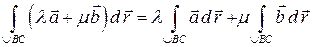 (свойство линейности),
(свойство линейности),
2) 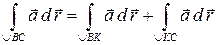 (свойство аддитивности),
(свойство аддитивности),
3) 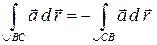 ,
,
т. е. при изменении направления обхода кривой линейный интеграл меняет знак, т. к. векторы 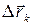 меняют свое направление на противоположное.
меняют свое направление на противоположное.
Выразив скалярное произведение векторов 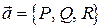 и
и 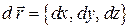 через их координаты, получим
через их координаты, получим
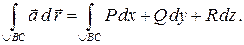
Выражение 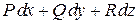 в скобки не заключают, хотя знак интеграла относится ко всему этому выражению. В формуле функции
в скобки не заключают, хотя знак интеграла относится ко всему этому выражению. В формуле функции 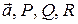 есть функции точки
есть функции точки 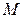 или ее координат
или ее координат 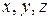 . Интеграл
. Интеграл 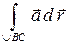 называют векторной формой, а интеграл
называют векторной формой, а интеграл  ─ координатной формой записи линейного интеграла.
─ координатной формой записи линейного интеграла.
В тех случаях, когда линейный интеграл поля  берется по замкнутой кривой
берется по замкнутой кривой 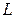 , он называется циркуляцией поля
, он называется циркуляцией поля  по кривой
по кривой 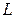 и обозначается так:
и обозначается так:
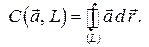
Приняты и другие обозначения циркуляции: 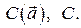
15. Лекционное занятие. ВЫЧИСЛЕНИЕ ЛИНЕЙНОГО ИНТЕГРАЛА
Правило вычисления линейных интегралов 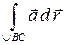 в следующих двух случаях.
в следующих двух случаях.
1). Для вычисления интеграла 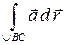 по линии
по линии 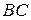 , заданной уравнениями
, заданной уравнениями 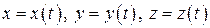 , следует:
, следует:
а) записать интеграл в координатной форме
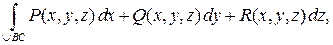
б) заменить 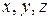 в функциях
в функциях 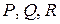 соответственно на
соответственно на 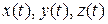 ,
,
в) заменить 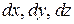 соответственно на
соответственно на 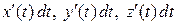 ,
,
г) найти интервал изменения параметра 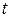 и вычислить получившийся определенный интеграл по этому интервалу.
и вычислить получившийся определенный интеграл по этому интервалу.
2). Для вычисления интеграла 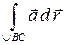 по плоской линии
по плоской линии 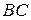 с уравнением
с уравнением 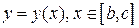 следует:
следует:
а) записать интеграл в координатной форме 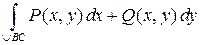 ,
,
б) заменить 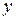 в функциях
в функциях 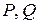 на
на 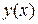 ,
,
в) заменить 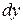 на
на 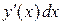 ,
,
г) вычислить получившийся определенный интеграл по отрезку 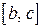 .
.
3). В случае центрального поля 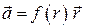 следует учесть, что
следует учесть, что 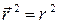 ; дифференцируя это равенство, получим
; дифференцируя это равенство, получим 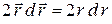 и
и
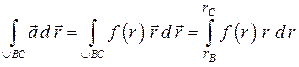
т.е. линейный интеграл поля сведен к определенному интегралу.
Пример 1. Вычислить работу силы 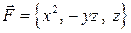 по прямолинейному перемещению из точки
по прямолинейному перемещению из точки 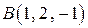 в точку
в точку 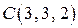 .
.
Решение. Работа 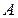 силы
силы 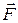 вычисляется по формуле
вычисляется по формуле
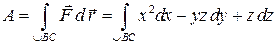 .
.
Для вычисления этого интеграла составим уравнение прямой 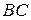 :
:
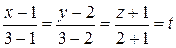 .
.
Отсюда 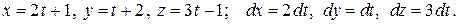
Найдем значение параметра 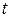 , соответствующее точке
, соответствующее точке 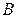 . Для этого подставим абсциссу
. Для этого подставим абсциссу 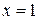 точки
точки 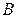 в формулу
в формулу 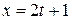 . Получим
. Получим 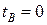 . Аналогично найдем
. Аналогично найдем 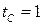 . Заменяя в интеграле
. Заменяя в интеграле 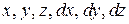 их выражениями, получим
их выражениями, получим
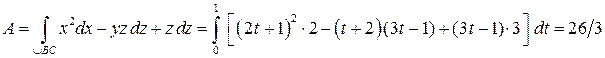 .
.
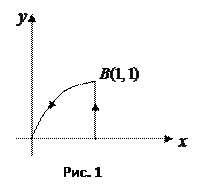 Пример 2. Найти циркуляцию поля
Пример 2. Найти циркуляцию поля 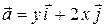 вдоль линии
вдоль линии 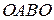 , где
, где 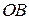 ─ дуга параболы
─ дуга параболы 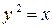 ,
,  ─ ломаная (рис. 1).
─ ломаная (рис. 1).
Решение. Циркуляцию поля  вычислим по формуле
вычислим по формуле
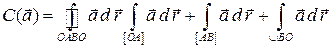 .
.
На отрезке 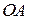 имеем
имеем 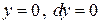 . Поэтому
. Поэтому
|
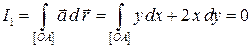 .
. На отрезке 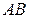 имеем
имеем 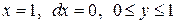 . Поэтому
. Поэтому
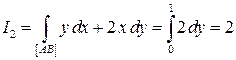 .
.
На дуге 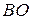 имеем
имеем 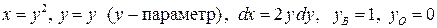 . Поэтому
. Поэтому
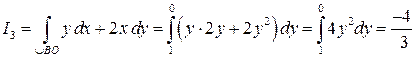 .
.
Окончательно, 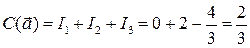 .
.
Пример 3. Вычислить циркуляцию поля  по окружности
по окружности 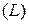 радиусом
радиусом 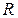 с центром в начале координат, ориентированной против часовой стрелки.
с центром в начале координат, ориентированной против часовой стрелки.
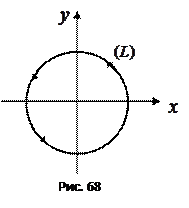 Решение. Циркуляция поля
Решение. Циркуляция поля  вычисляется по формуле
вычисляется по формуле

 .
.
|
 Для вычисления этого интеграла запишем параметрические уравнения окружности
Для вычисления этого интеграла запишем параметрические уравнения окружности 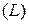 :
: 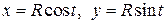 .
.
|
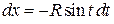 ,
, 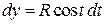 ; угол
; угол 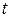 при движении против часовой стрелки меняется от
при движении против часовой стрелки меняется от 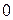 до
до 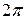 (рис. 2). Поэтому
(рис. 2). Поэтому 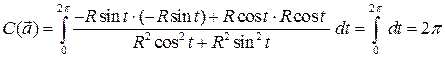 .
. 2014-02-02
2014-02-02 4442
4442