Частотные характеристики ДИНАМИЧЕСКИХ звеньев и систем автоматического управления.
В основу методов исследования и расчета систем автоматического управления положены частотные характеристики звеньев направленного действия. Частотные характеристики показывают, как изменяются амплитуда и фаза выходного гармонического сигнала звена направленного действия относительно входного в зависимости от частоты этого сигнала. Частотные характеристики могут рассматриваться не только для простейших звеньев, но и сложных функциональных элементов или САУ в целом.
Рассматривается передача линейным звеном направленного действия гармонического сигнала x (ω t) cамплитудой Аx, угловой частотой ω, начальной фазой θ x:
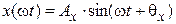 .
.
На выходе звена в установившемся режиме гармонический сигнал y (ω t) имеет ту же частоту, но изменившиеся амплитуду Аy и фазу θ y:
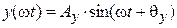 .
.
Изменения гармонического сигнала при передаче его звеном можно характеризовать отношением амплитуд 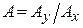 и разностью фаз ψ = θ у –θ х.
и разностью фаз ψ = θ у –θ х.
Если угловую частоту гармонического сигнала изменять в широком диапазоне, можно получить зависимость относительного изменения амплитуды А (ω) и фазы ψ(ω) сигнала при передаче его звеном, функциональным элементом или системой. Такие зависимости называют амплитудно-частотными (АЧХ) и фазо-частотными (ФЧХ) характеристиками.
Гармонические сигналы x (ω t) и y (ω t) можно представить на комплексной плоскости в виде векторов 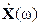 ,
, 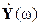 , вращающихся с угловой частотой ω. Модуль каждого вектора равен амплитуде соответствующего сигнала, а их положение на комплексной плоскости определяется начальными фазами. Векторы этих сигналов в комплексной форме имеют следующее выражение:
, вращающихся с угловой частотой ω. Модуль каждого вектора равен амплитуде соответствующего сигнала, а их положение на комплексной плоскости определяется начальными фазами. Векторы этих сигналов в комплексной форме имеют следующее выражение:
 ;
;
 .
.
Комплексной частотной функцией (комплексным коэффициентом передачи) называют отношение векторавыходного гармонического сигнала 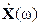 к вектору входного сигнала
к вектору входного сигнала 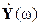 :
:
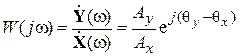 .
.
Таким образом, комплексная частотная передаточная функция характеризует относительное изменение амплитуды А и фазы ψ гармонического сигнала при передаче его звеном или системой. На комплексной плоскости частотную передаточную функцию можно представить вектором 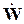 :
:

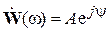 .
.
Модуль вектора 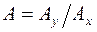 есть отношение амплитуд, а фаза вектора ψ = θy – θx – разность фаз входного и выходного гармонических сигналов.
есть отношение амплитуд, а фаза вектора ψ = θy – θx – разность фаз входного и выходного гармонических сигналов.
При анализе частотных характеристик более удобной является алгебраическая форма записи комплексной частотной функции с выделением вещественной Re W (j w) и мнимой Im W (j w) частей:
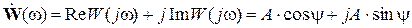 .
.
При обратном преобразовании для определения модуля и фазы вектора комплексной частотной функции используют известные соотношения:
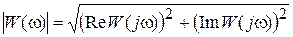 ;
;
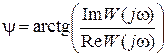 .
.
 2014-02-02
2014-02-02 3695
3695
