Пример 2.5

Процесс в объекте описывается дифференциальным уравнением 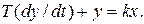Найти переходную функцию.

Вводим условие единичного ступенчатого воздействия, полагая x = 1. Ищем решение дифференциального уравнения при нулевых начальных условиях. Решением будет переходная функция h (t), поэтому сразу можно y (t) заменить на h (t).

Общее решение неоднородного уравнения

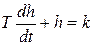
есть сумма решений h ₁ + h ₂. Первое получают, решая однородное уравнение

.

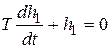Решением будет 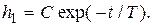Второе решение h ₂ есть частное решение неоднородного уравнения, которое можно выбрать как h ₂ = k. Общим решением будет:

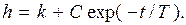
C учетом того, что h = 0 при t = 0, окончательное выражение для переходной функции получается в виде:

.

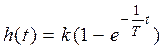Найти переходную функцию для системы, описываемой дифференциальным уравнением

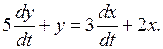
Запишем операторное уравнение

(5 p + 1) Y (p) = (3 p + 2) X (p)

в виде

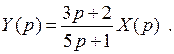
Множитель при X (p) есть не что иное, как передаточная функция. X (p) – изображение произвольного воздействия. Воздействие в виде единичного ступенчатого скачка имеет изображение X (p) = 1/ p. Если в операторном уравнении заменить X (p) на 1/ p, то на Y (p) накладывается требование быть изображением переходной функции. Подчеркивая это, заменим Y (p) на H (p). Получаем операторное уравнение для переходной функции:

.

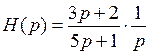Прежде чем воспользоваться таблицей изображений по Лапласу, представим правую часть уравнения в виде суммы:

.

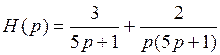В таблице находим оригиналы по их изображениям:

,

,

.

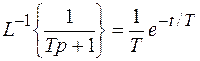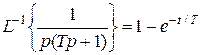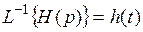В нашем случае T = 5. Множители 3 и 2 сохраняют свое значение и место. Окончательно

,

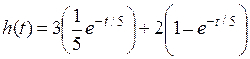или

h (t) = 2 – 1,4e ^{- t / 5}.