Усилительное звено

Литература

1. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.

2. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Наука, 1989. – 304 с.

3. МакаровИ.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). – М.: Машиностроение, 1977. – 464 с.

4. Гноенский Л.С., Каменский Г.С., Эльсгольц Л.Э. Математические основы теории управляемых систем. – М.: Наука, 1969.

Системы автоматического регулирования удобно представлять в виде соединения элементов, каждый из которых описывается алгебраическим или дифференциальным уравнением не выше второго порядка. При этом, одно и то же дифференциальное уравнение может описывать разные по своей физической природе элементы. Иными словами, у них одна математическая модель. Наиболее употребительные математические модели получили название типовых звеньев. Типовые звенья имеют одну входную и одну выходную величину.

Все конструктивное разнообразие САР можно представить небольшим числом типовых звеньев или их комбинаций.

Рассмотрим следующие типовые звенья.

Звенья, описываемые алгебраическими уравнениями:

- усилительное (пропорциональное),

- запаздывающее.

Звенья, описываемые дифференциальным уравнением первого порядка:

- инерционное,

- интегрирующее,

- дифференцирующее.

Звено, описываемое дифференциальным уравнением второго порядка. В зависимости от соотношения коэффициентов, оно может быть колебательным или апериодическим.

Характеристики типовых звеньев принято указывать для единичного ступенчатого входного воздействия.

Для полной характеристики типового звена следует указать его дифференциальное уравнение, операторное уравнение, передаточную функцию, комплексную, действительную, мнимую, амплитудную, фазовую, логарифмическую амплитудную, логарифмическую фазовую частотные характеристики и переходную функцию.

У этого звена выходная величина y (t) пропорциональна входной. Поэтому усилительное звено называют еще пропорциональным. Математическая модель

y (t) = k x (t), (3.1)

где константа k - коэффициент усиления звена.

Операторное уравнение

Y (p) = k X (p).

Передаточная функция представляет собой коэффициент усиления:

K (p) = 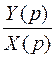= k.

(Здесь и далее передаточную функцию типового звена будем обозначать K (p)).

Комплексная частотная характеристика имеет только действительную часть:

K (jw) = k.

Формально, в соответствие с формулой (2.9), K (jw) = U (w) + jV (w). Действительная частотная характеристика U (w) = k, мнимая частотная характеристика V (w) = 0.

Амплитудная частотная характеристика:

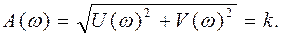
Она не зависит от w - входной сигнал любой частоты изменяется в k раз.

Фазовая частотная характеристика:

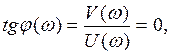
φ (ω) = arctg 0 = 0.

Фазовый сдвиг отсутствует.

Логарифмическая амплитудная частотная характеристика имеет вид:

L (ω) = 20lg A (ω) = 20lg k.

От ω, следовательно и от lg ω, не зависит. (Прямая, параллельная оси абсцисс).

Переходную функцию усилительного звена получают, положив x = 1(t) в уравнении y = kx. Переходная функция h (t) = k× 1(t).

Регулирование объекта осуществляется с помощью устройств, динамические характеристики которых могут быть близкими или идентичными характеристиками типовых звеньев. В частности, используются регуляторы с характеристиками усилительного звена. Их называют П-регуляторы, имея ввиду пропорциональность входной и выходной величин.