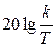Инерционное звено

Другое название - апериодическое звено первого порядка. Описывается дифференциальным уравнением

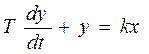, (3.3)

где Т – постоянная времени звена, k – коэффициент усиления.

Операторное уравнение

(Tp + 1) Y (p) = kX (p).

Передаточная функция

.

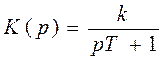При p = 0 передаточная функция вырождается в коэффициент усиления. (p = 0 означает отсутствие изменения выходной величины, dy / dt = 0, что превращает инерционное звено в усилительное).

Комплексная частотная характеристика

.

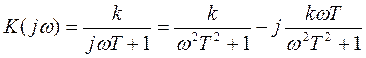Действительная и мнимая частотные характеристики

, .

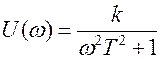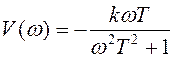При w = 0 амплитуда равна коэффициенту усиления, с увеличением w стремится к нулю.

Амплитудная частотная характеристика:

.

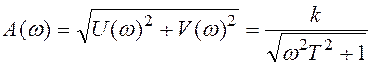Фазовая частотная характеристика:

.

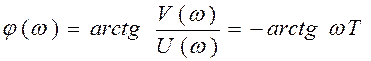Она представляет собой кривую, асимптотически приближающуюся к величине j (¥) = –p/2.

Логарифмическая амплитудная частотная характеристика:

.

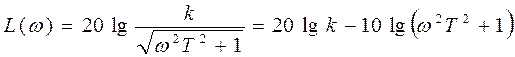Найдем асимптотические прямые логарифмической амплитудной частотной характеристики. В области низких частот, w < 1, асимптотой будет 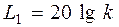. В области высоких частот, w > 1, асимптотой будет 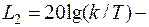20lg w. Прямая L ₂ пересекает ось абсцисс при lg w = lg(k / T), ось ординат при lg w = 0; L ₂ = 20 lg (k / T). Прямые L ₁ и L ₂ пересекаются в точке сопряжения. Приравняв 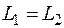, найдем частоту сопряжения: 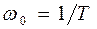. (Ее также называют собственной частотой инерционного звена). Общий вид графика представлен на рис.3.2.

L (w)

L ₂

L ₁ 20lg k

0 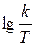lg w

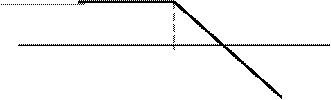
Рис. 3.2. Общий вид асимптот ЛАЧХ инерционного звена

Переходная функция находится как решение уравнения (3.3) при x = 1 и у (0) = 0:

.

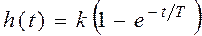h (t) возрастает экспоненциально и стремится стать равной k при t ® ¥.

Пример 3.1.

Построить график комплексной частотной характеристики инерционного звена для k = 10, Т = 0,1.