Запаздывающее звено. В запаздывающем звене выходная величина начинает изменяться не мгновенно с воздействием входной величины

В запаздывающем звене выходная величина начинает изменяться не мгновенно с воздействием входной величины, а некоторое время t спустя.

Уравнение звена:

y (t) = kx (t - τ), (3.2)

где τ – время запаздывания.

Изображение функции с запаздывающим аргументом x (t - τ) по Лапласу есть 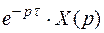. Следовательно, операторное уравнение будет

.

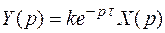
Передаточная функция звена

.

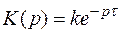
Комплексная частотная характеристика, если раскрыть ее формулой Эйлера через тригонометрические функции,

.

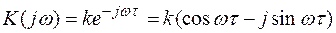Действительная частотная характеристика U (ω) = k cos ωτ, мнимая частотная характеристика V (ω) = – k sin ωτ.

Амплитудная частотная характеристика – постоянная величина:

.

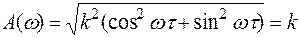Амплитуда не зависит от частоты, входной сигнал не изменяется.

Составляя 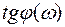, обнаруживаем, что

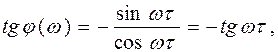
откуда фазовая частотная характеристика:

φ (ω) = – ω τ.

Для фиксированного времени запаздывания τ зависимость от частоты линейная. Запаздывание по фазе нарастает с увеличением частоты.

Логарифмическая амплитудная частотная характеристика

L (w) = 20 lg A (w) = 20 lg k.

Переходная функция запаздывающего звена h (t) = k ×1(t - t). На выходе звена получается скачок спустя t секунд после воздействия на входе, рис. 3.1.

h (t)

k

0 t t

	Рис. 3.1. Переходная функция запаздывающего звена