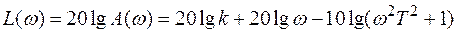Логарифмическая амплитудная частотная характеристика. Найдем асимптотические прямые логарифмической амплитудной частотной характеристики

.

Найдем асимптотические прямые логарифмической амплитудной частотной характеристики. В области w < 1 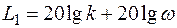. В области w > 1 L ₂ = 20 lg (k / T)

Прямая L ₁ пересекает ординату в точке с координатами lg w = 0, L ₁ = 20 lg k, абсциссу – в точке с координатами lg w = lg(1 / k), L ₁ = 0. Cледует учесть, что k > 1 и потому lg(1 / k) – число отрицательное. Прямая L ₂ параллельна оси абсцисс, пересекает ординату в точке lg w = 0, L ₂ = 20lg(k / T). Прямые L ₁ и L ₂ пересекаются в точке с абсциссой lg w = lg(1 / T). График представлен на рис. 3.6.

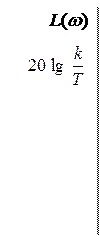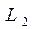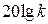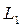
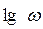0

Рис. 3.6. Асимптоты ЛАЧХ

реального дифференцирующего звена.

Чтобы найти переходную функцию, в операторном уравнении заменим X (p) на 1/ p:

.

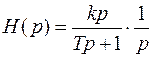Таблица преобразований Лапласа указывает, что

.

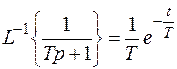Значит, переходная функция имеет вид

.

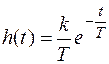В момент t = 0 h (0) = k / T. По мере увеличения t, функция h (t) экспоненциально уменьшается до нуля. Напомним: в идеальном дифференцирующем звене переходная функция имеет вид импульса.