Сначала рассмотрим идеальное дифференцирующее звено. Дифференциальное уравнение этого звена устанавливает пропорциональность выходной величины скорости изменения входной величины:
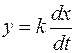 . (3.5.)
. (3.5.)
Операторное уравнение: Y (p) = kp X (p).

где k – коэффициент усиления.
Комплексная частотная характеристика
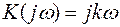 .
.
Действительная часть U (w) = 0, мнимая часть V (w) = kw.
Амплитудная частотная характеристика
 .
.
Амплитуда растет линейно с частотой.
Фазовый угол для всех частот 90°, что означает постоянное опережение по фазе при любой частоте.
Переходная функция – в ответ на единичное ступенчатое воздействие – имеет вид:
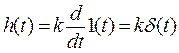 .
.
То есть, на выходе появляется единичный импульс, усиленный в k раз.
Осуществить практически идеальное дифференцирующее звено невозможно. Но реализуемы математические модели, в которых присутствует дифференцирующая составляющая dx / dt. Так, если записать в правой части инерционного звена вместо усилительного дифференцирующее воздействие, получается математическая модель, которую называют «реальное дифференцирующее звено».
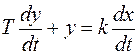 . (3.6)
. (3.6)
Операторное уравнение: (Tp + 1) Y (p) = kpX (p).
Передаточная функция
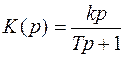 .
.
 2014-02-02
2014-02-02 1008
1008








