Прямая в пространстве. Определение прямой как геометрического места таких точек, что отрезок, соединяющий любые две из них, параллелен заданному вектору, сохраняется и для случая пространственных прямых. Единственная разница в том, что заданный вектор 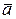 имеет уже три координаты
имеет уже три координаты 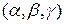 , заданная точка прямой
, заданная точка прямой 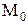 имеет три координаты
имеет три координаты 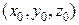 , и переменная точка прямой M также имеет три координаты
, и переменная точка прямой M также имеет три координаты 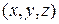 .
.
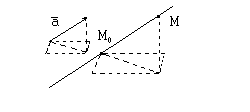
Поэтому, используя подобие соответствующих треугольников, мы вместо соотношения (1) получим двойное равенство
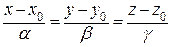 . (2)
. (2)
Приравнивая все части (2) переменной 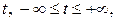 мы получим параметрическое уравнение пространственной прямой:
мы получим параметрическое уравнение пространственной прямой:
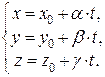
Второй способ задания пространственной прямой – как геометрическое место точек пересечения двух плоскостей – мы сможем использовать после знакомства с плоскостями.
Плоскость. Простейшей из пространственных поверхностей является плоскость – геометрическое место таких точек, что отрезок, соединяющий любые две из них, перпендикулярен данному вектору, называемому нормалью к плоскости.
Зададим плоскость с данной нормалью 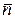
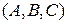 с помощью точки
с помощью точки 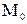 с координатами
с координатами 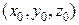 , лежащей в этой плоскости.
, лежащей в этой плоскости.
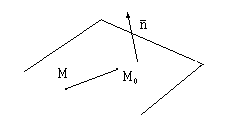

Если взять произвольную, отличную от 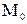 , точку M с координатами
, точку M с координатами 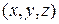 в данной плоскости, то согласно определению и условию взаимной перпендикулярности двух векторов имеем
в данной плоскости, то согласно определению и условию взаимной перпендикулярности двух векторов имеем 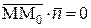 . Используя координаты этих векторов получим условие взаимной перпендикулярности в виде
. Используя координаты этих векторов получим условие взаимной перпендикулярности в виде 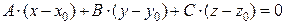 .
.
Последнее уравнение и есть уравнение плоскости, проходящей через данную точку. В частности, уравнения плоскостей, параллельных координатным плоскостям, имеют вид 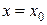 ,
, 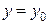 или
или 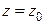 .
.
В случае, когда какой-то из коэффициентов уравнения плоскости отличен от нуля, можно выразить соответствующую координату через две другие координаты, например,  при
при  . Такое уравнение может считаться параметрическим заданием плоскости, где в качестве двух независимых параметров выступают две из координат, а третья линейно выражается через два параметра.
. Такое уравнение может считаться параметрическим заданием плоскости, где в качестве двух независимых параметров выступают две из координат, а третья линейно выражается через два параметра.
Плоскость в пространстве может задаваться не только нормалью и одной точкой, но и тремя различными точками, с координатами 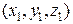 ,
, 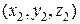 и
и 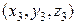 , через которые она проходит.
, через которые она проходит.
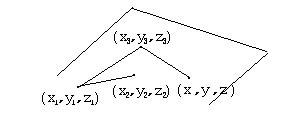
Рассматривая три вектора, лежащие в одной плоскости, получим в соответствии со свойством смешанного произведения соотношение 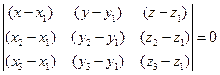 . Если раскрыть определитель по способу, указанному выше, получим линейную комбинацию разностей
. Если раскрыть определитель по способу, указанному выше, получим линейную комбинацию разностей 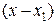 ,
, 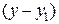 и
и 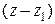 , то есть линейное уравнение относительно координат переменной точки плоскости
, то есть линейное уравнение относительно координат переменной точки плоскости 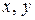 и
и 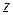 .
.
 2014-02-02
2014-02-02 1607
1607
