Перенос сумматора с входа звена на выход

Исходная схема имеет два входных сигнала Х ₁ и Х ₂ и один выходной сигнал Х ₄, рис. 14 а. Выходной сигнал связан с входными уравнением Х ₄ = К Х ₃ = К Х ₁ + К Х ₂. Эквивалентная схема должна иметь те же входные и выходной сигналы.

Чтобы получить тот же сигнал Х ₄, в линию входного сигнала Х ₂ следует ввести корректирующее звено с передаточной функцией К_к. Тогда сигнал Х ₄ окажется связанным с входными сигналами уравнением:

Х ₄ = Y ₁ + Y ₂ = К Х ₁ + К_к Х ₂.

Х ₁ Х ₃ Х ₄ Х ₁ Y ₁ Х ₄

К К

Х ₂ Х ₂ Y ₂

К ₁

Рис. 14 а. Система до Рис. 14 б. Эквивалентная структурная

перестановки. схема.

Сравнивая его с уравнением Х ₄ = К Х ₁ + К Х ₂ для исходной схемы, приходим к заключению, что корректирующая передаточная функция К_к = К. Что и обозначено на схеме рис. 14 б.

Перенос сумматора с входа звена на выход, при условии сохранения входных и выходных сигналов системы, требует включения в линию второго подаваемого на сумматор сигнала звена, с передаточной функцией, одинаковой с заданной.

Пример 4.10.

Найти передаточную функцию системы, структурная схема которой изображена на рис. 15.

Х С ₁ С ₂ 1 С ₃ 2 С ₄ 3 4 Y

К ₁ К ₃ К ₅

К ₂ К ₄

К ₆

К ₇

Рис. 15. Исходная структурная схема.

Звенья с передаточными функциями К ₃ и К ₄ соединены параллельно. Сделаем первое упрощение схемы, заменив их передаточной функцией 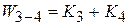. Из схемы устраняются узел 2 и сумматор С ₄. Также переставим сумматоры С ₁ и С ₂. Схема примет вид:

Х С ₂ С ₁ 1 С ₃ 3 4 Y

К ₁ W _3-4 К ₅

К ₂ К ₆

К ₇

Обнаруживаем, что звено с передаточной функцией К ₁ охвачено положительной обратной связью через звено с передаточной функцией К ₂. Схема упрощается, если ввести передаточную функцию 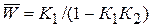. Сумматор С ₁ и узел 1 устраняются. Остается:

Х С ₂ С ₃ 3 4 Y

W _3-4 К ₅

К ₆

К ₇

Дальнейшее упрощение схемы связано с переносом узла 4 с выхода звена К ₅ на его вход и перестановкой с узлом 3. В ответвлении от узла 4 появляется звено К ₅, последовательно включенное со звеном К ₆.

X С ₂ С ₃ 4 3 Y

W _3-4 К

К ₆ К ₅

К ₇

Обнаруживается замкнутый контур из звеньев с передаточными функциями W _3-4, К ₅ и К ₆. Его можно заменить звеном с передаточной функцией 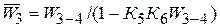. Сумматор С ₃ и узел 4 устраняются. Схема приобретает вид:

Х С ₂ 3 Y

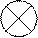
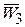К ₅

К ₇

Выражая последний замкнутый контур звеном 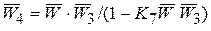, приходим к схеме

Х Y

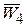К ₅

Следовательно, передаточная функция системы, имеющей структурную схему, показанную на рис. 15, есть

,

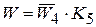или, в развернутом виде,

.

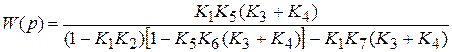Литература

1. Бесекерский В.А., Попов Е.П. Теория автоматического управления. – СПб, изд-во «Профессия», 2004. – 752 с.

2. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.

3. Макаров И.М., Менский Б.М. Линейные автоматические системы. – М.: Машиностроение, 1947 –464 с.

4. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. – М.: Машиностроение, 1973 – 606 с.