Устойчивость системы выясняется по характеристическому полиному передаточной функции:
D (p) = a 0 pn + a 1 pn -1 + …+ a n-1 p + an, (2.5)
где n – степень полинома.
Полагая p = jw, преобразуем характеристический полином в комплексный частотный полином:
D (jω) = a0(jω)n + a1(jω)n-1 +…+ an-1(jω) + an.
В зависимости от степени числа (jω)n оно либо действительное, либо мнимое. По этой причине частотный полином распадается на действительную часть U (ω) и мнимую часть V (ω):
D (jω) = U (ω) + j V (ω), (5.7)
U (ω) = an - an-2ω2 + an-4ω4 - … (5.8)
V (ω) = an-1ω - an-3ω3+an-5ω5 -…. (5.9)
U (ω) – четная функция ω, V (ω) – нечетная функция ω. По этому признаку полиномы (5.8) и (5.9) можно назвать «четный» и «нечетный».
Задавая какое-либо значение частоты w 1, из (5.8) и (5.9) получим числа U (w 1) и V (w 1). Вместе они образуют комплексное число D (jw 1). На комплексной плоскости оно обозначается точкой М(U, V), рис. 5.1. Множество точек М(U, V), отвечающих разным частотам, образуют кривую, которая называется годографом Михайлова.
Рассмотрим годографы Михайлова для устойчивых систем.
В случае устойчивых систем годограф Михайлова имеет свойство начинаться с точки U (0) = an, V (0) = 0, рис. 5.1. По мере увеличения w от нуля до бесконечности, точка М(U, V) перемещается влево так, что кривая стремится охватить начало координат, одновременно удаляясь от него. Если провести радиус-вектор из начала координат в точку М(U, V), то окажется, что радиус-вектор будет поворачиваться против часовой стрелки, непрерывно увеличиваясь. Непрерывно увеличивается и угол, который он образует с осью абсцисс. Представив комплексное выражение (5.7) в экспоненциальной форме,
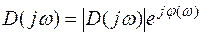 ,
,
обнаруживаем, что радиус-вектор есть модуль комплексного частотного полинома | D (jw)|, а угол j (w) – аргумент. Модуль имеет величину 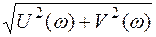 , аргумент равен
, аргумент равен 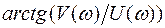 .
.
Вид годографа Михайлова зависит от степени n характеристического полинома (2.5). Годографы полиномов первых четырех степеней показаны на рис. 5.2. Они соответствуют устойчивым системам. Анализ годографов устойчивых систем позволяет сделать выводы, которые и составляют содержание критерия Михайлова.
Можно дать три формулировки критерию Михайлова.
Первая формулировка. Если при изменении частоты от нуля до бесконечности годограф Михайлова начинается на действительной оси в точке an,последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, не проходя через ноль, и уходит в бесконечность в n -м квадранте, - система устойчива.

 V(w) V
V(w) V

 n = 2
n = 2
n = 1

 n = 3
n = 3


 V M(U, V)
V M(U, V)
 | |||
| |||
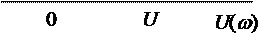
n = 4
Рис.5.1. Рис. 5.2.
Вторая формулировка. Если при изменении частоты от нуля до бесконечности вектор комплексного частотного полинома D (jw) последовательно поворачивается против часовой стрелки на угол n (p/2), где n – степень характеристического полинома, и нигде не становится нулем, - система устойчива.
Обратим внимание на частоты, при которых годограф пересекает оси координат. Назовем их «частоты пересечения». Первая частота нулевая, с нее начинается годограф. При w 1 = 0 U (0) = an, V (0) = 0. Вторая отвечает точке пересечения годографом положительного отрезка оси ординат, U (w 2) = 0, V(w 2) – некоторое число. Непрерывно увеличивая частоту, при некоторой, равной w 3, получим пересечение годографа с отрицательной частью оси абсцисс. Очевидно, четвертым будет пересечение с отрицательной частью оси ординат при частоте w 4. Далее последуют частоты пересечения w 5, w 6, …, wn. Все они действительные положительные числа, каждое последующее больше предыдущего.
Третья формулировка критерия Михайлова: если частоты пересечения годографа с осями координат чередуются и образуют возрастающую последовательность вида ω 1 < ω 2 < ω 3 <…< wn, - система устойчивая.
В отличие от предыдущих, третья формулировка позволяет исследовать устойчивость системы без построения годографа, аналитически. Соображения следующие.
Каждому пересечению годографом действительной оси (когда V (w) = 0) будет соответствовать корень нечетного полинома V (w). Каждому пересечению мнимой оси (когда U (w) = 0) будет соответствовать корень четного полинома U (w). Следовательно, по мере увеличения w корни полиномов V (w) и U (w) для устойчивой системы должны чередоваться (корень полинома V (w) сменяется корнем полинома U (w) и т.д.); корень каждого последующего пересечения оси должен быть больше предыдущего, все корни должны быть действительными. Общее число корней равно степени характеристического полинома.
В случае неустойчивых систем кривые не охватывают начало координат, чередования частот нечетного и четного полиномов нет, рис. 5.3.
 V
V

 V
V

 n = 3 n = 4
n = 3 n = 4
 n = 4 n = 3
n = 4 n = 3
|


|
|


n = 1
|
Рис. 5.3. Рис. 5.4.
Если годограф начинается из начала координат или проходит через начало координат, система находится на границе устойчивости, рис. 5.4.
Построить годограф Михайлова для характеристического уравнения
2 p + 1 = 0.
Имеем: D (jw) =1 + j 2 w, U (w) = 1, V (w) = 2 w, | D (jw)| = 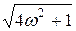 , tg j = 2 w. Полагая V (w) = 0, получаем начало годографа: | D (jw)| = 1. В пределах 0 £ w £¥ угол меняется от j = 0 до j = p/2, т.е. вектор D (jw) поворачивается против часовой стрелки один раз на p/2. При этом, V (w) растет, а U (w) остается равным 1. Годограф получается в виде прямой, параллельной мнимой оси, рис. 5.5.
, tg j = 2 w. Полагая V (w) = 0, получаем начало годографа: | D (jw)| = 1. В пределах 0 £ w £¥ угол меняется от j = 0 до j = p/2, т.е. вектор D (jw) поворачивается против часовой стрелки один раз на p/2. При этом, V (w) растет, а U (w) остается равным 1. Годограф получается в виде прямой, параллельной мнимой оси, рис. 5.5.
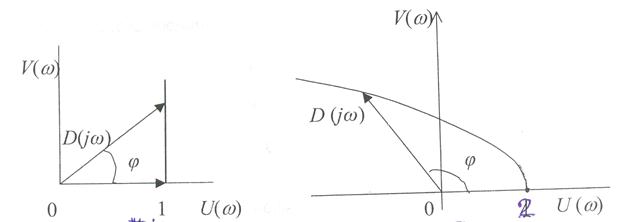
Рис. 5.5. n = 1. Рис. 5.6. n = 2.
Выяснить устойчивость системы с характеристическим уравнением второй степени
9 p 2 + 4 p + 2 = 0.
Комплексный частотный полином, его действительное и мнимое слагаемые имеют вид:
D (jw) = - 9 w 2 + j 4 w + 2,
U (w) = 2 – 9 w 2,
V (w) = 4 w.
Полагая V (w) = 0, находим: первая частота пересечения w 1 = 0. Годограф начинается в точке U (w 1) = 2. Пересечение годографа с мнимой осью задается уравнением U (w) = 0. Находим: вторая частота пересечения w 2 = ~0,47. Ордината пересечения V (w 2) ~ 1,9. Во втором квадранте, с увеличением частоты, годограф уходит в бесконечность. График показан на рис. 5.6.
Годограф проходит первый квадрант и уходит в бесконечность во втором. Вектор D (jw) поворачивается на угол, равный степени характеристического уравнения, умноженной на p/2: Корни действительные, w 1 < w 2 и требование последовательного возрастания частот пересечения выполняется. Следовательно, система устойчива.
 2014-02-02
2014-02-02 1365
1365
