Дана система, характеристическое уравнение которой имеет вид:
T 1 T 1 T 2 T 3 p 3 + (T 1 T 2 + T 1 T 3 + T 2 T 3) p 2 + (T 1 + T 2 + T 3) p + 1 + k = 0.
Выяснить, будет ли система устойчивой, если T 1 = 1, T 2 = 2, T 3 = 3, k = 19? Каким должен быть коэффициент усиления на границе устойчивости?
Записываем характеристическое уравнение 3-й степени в общем виде, сопоставляем его с заданным и заключаем:
a0= T1T2T3 , a2= T1+T2+T3,
a1= T1T2+T1T3+T2T3 , a3= 1 +k.
Все коэффициенты больше нуля, но надо проверить, будет ли определитель Гурвица больше нуля. Подставив числа в неравенство a 1 a 2 - a 0 a 3> 0, обнаруживаем, что оно не выполняется: 66 - 120 < 0. Определитель оказался отрицательным. Следовательно, система неустойчива.
На границе устойчивости a 1 a 2 - a 0 a 3= 0. Подставляя числа, имеем: 11·6 = 6 (1 + k). Коэффициент усиления на границе устойчивости k = 10.
Выяснить, будет ли устойчивой система с характеристическим уравнением
5 p 4 + p + 2 = 0.
Сопоставив данное уравнение с его общим видом, получаем:
a 0 = 5, a 1 = a 2 = 0, a 3 = 1, a 4 = 2.
По условию устойчивости a 1 a 2 a 3 – a 12 a 4 – a 0 a 32 > 0. Это не выполняется:
-5∙12 < 0. Система неустойчива, хотя все коэффициенты положительные.
Звенья, передаточные функции которых
 и
и 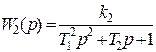 ,
,
соединяются последовательно. Выяснить, будет ли такая система устойчивой? Какую величину имеет постоянная времени T 0 на границе устойчивости замкнутой системы?
Находим передаточную функцию разомкнутой системы
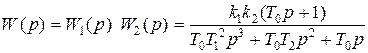 .
.
Ее знаменатель, приравненный к нулю, есть характеристическое уравнение. После сокращения на T 0 характеристическое уравнение выглядит так:
T 12 p 3 + T 2 p 2 + p = 0.
Сопоставляя с записью характеристического уравнения в общем виде, делаем вывод:
a 0 = T 12, a 1 = T 2, a 2 = 1, a 3 = 0.
Для уравнения 3-й степени условия устойчивости требуют, чтобы
a 0, a 1, a 2, a 3 > 0, a 1 a 2 - a 0 a 3 > 0.
Это соблюдается: T 12 , T 2 , 1 > 0, T 2 – 0 ∙ T 12 > 0. Следовательно, разомкнутая система устойчива.
Составим характеристическое уравнение замкнутой системы. Это будет сумма полиномов числителя и знаменателя, приравненная к нулю:
T 0 T 12 p 3 + T 0 T 2 p 2 + T 0(k 1 k 2 + 1) p + k 1 k 2 = 0.
Выписываем коэффициенты:
a 0 = T 0 T 12, a 1 = T 0 T 2 , a 2 = T 0(k 1 k 2 + 1), a 3 = k 1 k 2 .
Выясняем устойчивость:
T 0 T 12, T 0 T 2 , T 0(k 1 k 2 + 1), k 1 k 2 > 0.
Замкнутая система будет устойчивой, если
T 0 T 2 (k 1 k 2 + 1) - k 1 k 2 T 12 > 0.
На границе устойчивости определитель равен нулю, из чего заключаем:
 .
.
 2014-02-02
2014-02-02 2104
2104








