Бесконечно малые и бесконечно большие функции

Определение 1. Функция 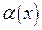называется бесконечно малой функцией (бесконечно малой) при 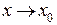, если .

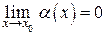Определение 2. Функция 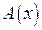называется бесконечно большой функцией (бесконечно большой) при 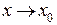, если .

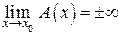Следствие. Функция 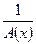при бесконечно малая, а 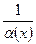- бесконечно большая.

Определение 3. Функции 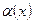и 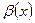называется бесконечно малыми одного порядка малости при , если 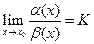, причем .

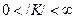Определение 4. Функции 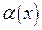и называется эквивалентными бесконечно малыми при 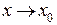, если .

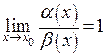Определение 5. Функция 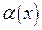называется бесконечно малой более высокого порядка малости, чем , при 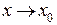, если .

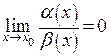Известны следующие свойства бесконечно малых.

1) Сумма конечного числа бесконечно малых – бесконечно малая.

2) Произведение бесконечно малой и конечной величины – величина бесконечно малая.

3) Произведение бесконечно малых – бесконечно малая.