Справедливы следующие формулы, называемые вторым замечательным пределом:

Равносильность этих формул следует из связи переменных: 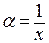 .
.
Мы получали число Непера 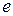 из подобной формулы, где была последовательность, а не функция. Заметим, что здесь в первой из приведенных формул переменная
из подобной формулы, где была последовательность, а не функция. Заметим, что здесь в первой из приведенных формул переменная  может стремиться как к
может стремиться как к 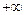 , так и к
, так и к 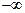 , а также может просто расти по абсолютной величине, меняя знак произвольно. Приведенная формула имеет следующие следствия.
, а также может просто расти по абсолютной величине, меняя знак произвольно. Приведенная формула имеет следующие следствия.
1. Если мы формально прологарифмируем вторую из приведенных формул, мы получим 1-е следствие второго замечательного предела:
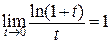 .
.
2. Другим следствие второго замечательного предела является предел, получаемый из предыдущего заменой 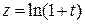 :
:
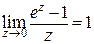 .
.
3. Рассмотрим теперь предел 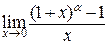 . Сделаем замену
. Сделаем замену 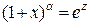 . При такой замене
. При такой замене 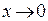 тогда и только тогда, когда
тогда и только тогда, когда 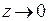 . Получим
. Получим
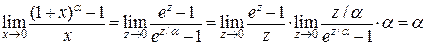
 2014-02-02
2014-02-02 1645
1645
