Докажем, что справедлива формула:
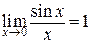 .
.
Прежде всего, заметим, что вследствие нечетности функции 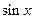 отношение
отношение 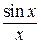 при
при 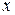 , близком к 0, положительно при любом знаке
, близком к 0, положительно при любом знаке 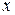 . Достаточно предположить, что
. Достаточно предположить, что 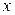 приближается к 0, оставаясь положительным. В противном случае мы сменим знак
приближается к 0, оставаясь положительным. В противном случае мы сменим знак 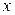 , что не повлияет на результат. Используем геометрическое доказательство. Рассмотрим сектор круга радиуса 1 с углом при вершине, равным
, что не повлияет на результат. Используем геометрическое доказательство. Рассмотрим сектор круга радиуса 1 с углом при вершине, равным 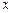 . BM – дуга граничной окружности сектора, A – его вершина, AB = AM = 1. BD – отрезок касательной к дуге BM в точке B. BC – перпендикуляр, опущенный из точки B на отрезок AM.
. BM – дуга граничной окружности сектора, A – его вершина, AB = AM = 1. BD – отрезок касательной к дуге BM в точке B. BC – перпендикуляр, опущенный из точки B на отрезок AM.
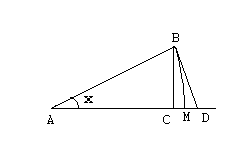
В силу последовательной вложимости друг в друга треугольника ABM, сектора ABM и треугольника ABD соответствующие соотношения имеют место между площадями этих фигур: 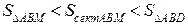 . Имеем
. Имеем 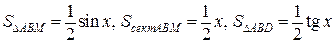 . Поэтому получаем неравенство
. Поэтому получаем неравенство  . Если мы поделим все части этого неравенства на
. Если мы поделим все части этого неравенства на 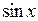 , то в силу предположения о знаке
, то в силу предположения о знаке 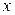 знаки неравенства не изменятся. Поэтому мы имеем
знаки неравенства не изменятся. Поэтому мы имеем 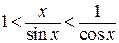 . А теперь устремим
. А теперь устремим 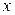 к нулю и применим теорему о двух полицейских. Мы получим
к нулю и применим теорему о двух полицейских. Мы получим 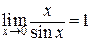 . Осталось применить свойство 5) пределов для получения предела обратной величины:
. Осталось применить свойство 5) пределов для получения предела обратной величины: 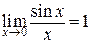 .
.
 2014-02-02
2014-02-02 350
350








