Пример 5.10

Дана передаточная функция разомкнутой системы:

.

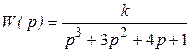Полагая k = 2 проверить с помощью критерия Найквиста, будет ли устойчивой замкнутая система?

Предварительно выясняем устойчивость разомкнутой системы по критерию Гурвица: система устойчива.

Найдем комплексную частотную характеристику:

.

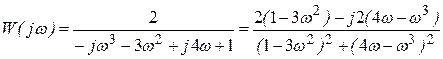Выделим действительный и мнимый частотные полиномы:

,

.

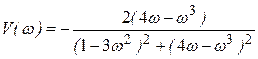Изменяя w от 0 до ¥, построим годограф разомкнутой системы.

По условию V(w) = 0 находим частоты пересечения годографом действительной оси и соответствующие значения U(w):

V(w) = 0, 4w - w³ = 0, w₁ = 0, w₂ = 2,

U(0) = 2. U(2) = -0,18.

Полагая U(w) = 0, находим частоту пересечения годографом мнимой оси и соответствующее значение V(w):

U(w) = 0, 1-3w² = 0, ,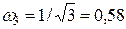

V(0,58) = -3,7 .

Для w = 1 получаем U(1) = -0,3, V(1) = -0,46 .

При w = ¥ U(¥) = 0, V(¥) = 0 .

Вид годографа показан на рис. 5.20.

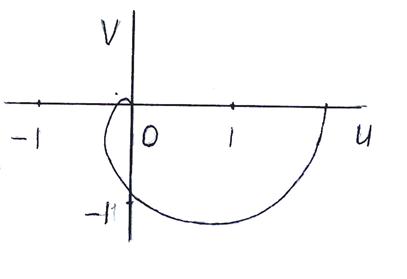
Рис. 5.20.

Разомкнутая система устойчивая, годограф не охватывает точку (-1,0), значит, замкнутая система тоже устойчивая.